|
The unique symbolical notation for links was introduced by J.Conway in 1967 [14]. From Conway symbols it is possible to read directly many of important knot or link properties: their symmetry, to recognize the world [15] to which they belong, to prove the equality of rational links [14] using very simple calculation, and even to derive some general conclusions: for example, all rational knots with symmetrical Conway symbol are amphicheiral [15]. Unfortunately, after the introduction of such fundamental concepts and the derivation of links with n£11 crossings, they are divided into disjoint classes: knots, 2-component links, 3-component links etc., and the universal classification principle is unavoidably lost. |

|
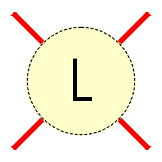
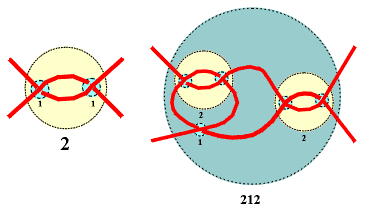
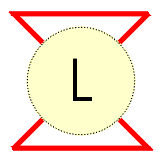
A tangle in a link projection is its region surrounded by a circle such that the link crosses the circle exactly four times, in the four points occuring in the four compass directions NW, NE, SW and SE. Two tangles are equivalent if one could be transformed into the other by a sequence of Redmeister moves. |
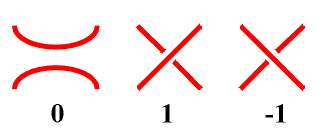
|
The elementary tangles are 0, 1 and -1, where for alternating links 0 and 1 are sufficient. |
|
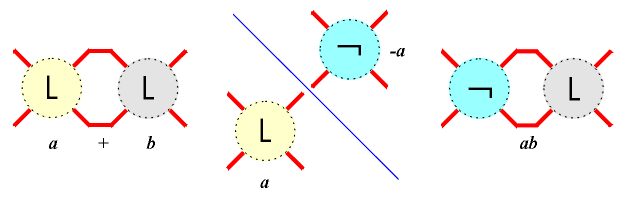
Tangles could be combined and modified by two operations: sum and product, leading from tangles a, b to the new tangles a+b, -a, ab, where -a is the image of a in NW-SE mirror, ab = -a+b, and -a = a0. |
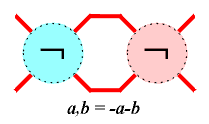
|
The third operation: ramification is defined as a,b = -a-b. That three operations are sufficient for the notation of links belonging to all worlds, except the polyhedral. |
|
As the numerator closure of a tangle we obtain the corresponding knot or link. |
|
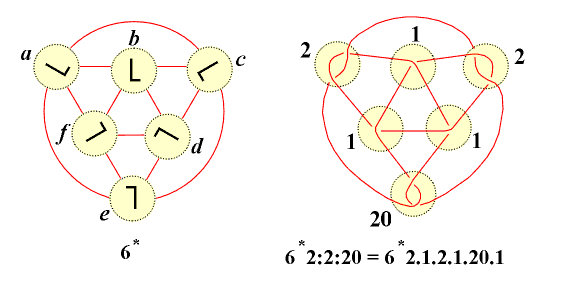
A link obtained from a basic polyhedron P* by substituting tangles t1,...,tk in appropriate places is denoted by P*t1...tk, where the number of dots between two successive tangles shows the number of omitted substituents of value 1. For example, 6*2:2:20 means 6*2.1.2.1.20.1 |
|
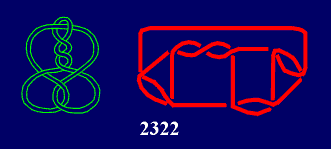
Together with the classical [13] ones, for the first time Conway symbols are used as the alternative notation in the book "Knots and Links" by D.Rolfsen, and after that undertaken by some other authors (e.g. C.C.Adams [10]). Anyway, if you try to draw some links from their Conway symbols, sometimes you will be surprised: projection obtained will be not isomorphic with that given by D.Rolfsen. For example, in the case of the knot 915, it is clear that from its Conway symbol 2322 we obtain the projection with 5, and not with 4 digons. |