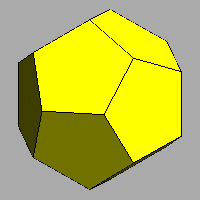







(only in m 3 5 point group)
hexecontahedron
(only in 235 point group)
Collection of the couples of archetypal
compound forms which are different in the
Livio Zefiro
Dip.Te.Ris., Universita' di Genova, Italy
(E-mail address: livio.zefiro@fastwebnet.it)
Notes
|
In two previous works [1,2] it has been shown that all the icosahedral compound forms belonging to the
holohedral m 3
5 point group can be derived
from the combination of seven single forms, corresponding to two Platonic and five Catalan
polyhedra; the same thing happens also in case of 235, the other icosahedral point group.
The only difference between the two point groups concerns the {hkl}
general form relative to each point group: in m 3
5 point group it is a hexakis-icosahedron, consisting of 120
faces, whereas in 235 point group it is a pentagonal hexecontahedron,
consisting of 60 faces.
The different multiplicity of the {hkl} general
forms depends on the lack, in the 235 point group, of both inversion centre
and mirror planes.
The other six forms (two Platonic and four Catalan polyhedra), coincide in the two point groups: as a matter of fact,
the number of faces belonging to each form does not vary, even in the presence of the fifteen mirror planes characterizing
the m 3
5
point group, since all the faces lie just in correspondence to the mirror planes.
| Platonic and Catalan single forms with icosahedral symmetry | |||
 |
 |
 |
 |
| 1) dodecahedron | 2) icosahedron | 3) rhomb-triacontahedron | 4) triakis-icosahedron |
 |
 |
 |
 |
| 5) deltoid-hexecontahedron | 6) pentakis-dodecahedron |
7') hexakis-icosahedron (only in m 3 5 point group) |
7") pentagonal hexecontahedron (only in 235 point group) |
Clicking by the left button of the mouse on the image of each polyhedron, one
can visualize the corresponding VRML dynamic image; analogously, the StereoNet
and the relative view along [001] can be visualized clicking on the name of each
polyhedron.
| |||
The entire collection of the 120
compound forms, belonging to
m 3
5
point group and derived from the two Platonic and the
five Catalan polyhedra, was reported in a recent work [3], where all the faces of
each compound form are equidistant from the centre of the
polyhedron.
The present work shows the sixty-three couples of compound forms which are different in
m 3
5
and 235 point groups, since they include, in combination with the other single forms,
either the hexakis-icosahedron or the pentagonal hexecontahedron
(which in turn give rise to a sixty-fourth couple, this time consisting in two single forms).
The other fifty-seven compound forms which do not include either the hexakis-icosahedron or the pentagonal hexecontahedron
are identical in the two icosahedral point groups; therefore, taking into account also the six single forms in common,
the forms shared by the two point groups are sixty-three altogether.
In this work the compound forms shared by the two point groups are not reported, since they
were
already shown in [3].
 |
 |