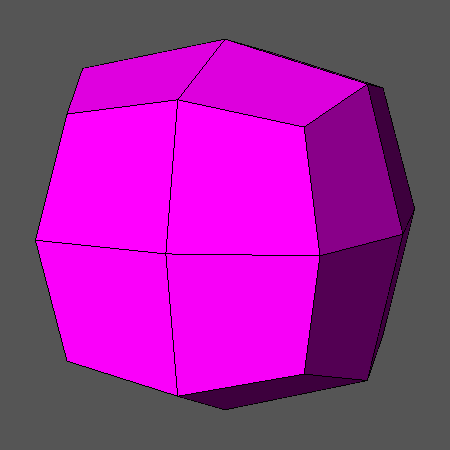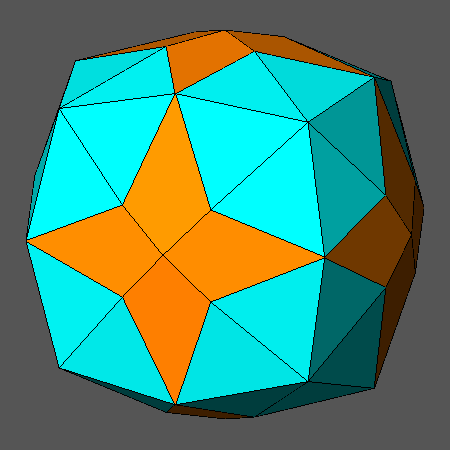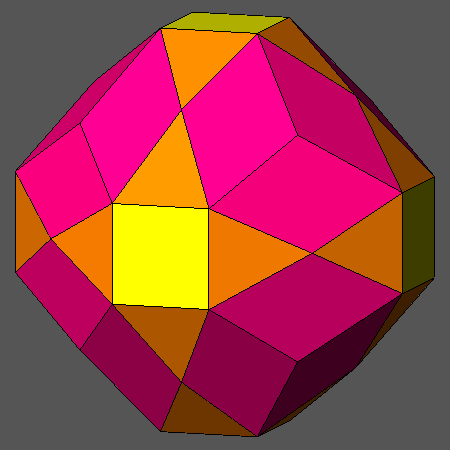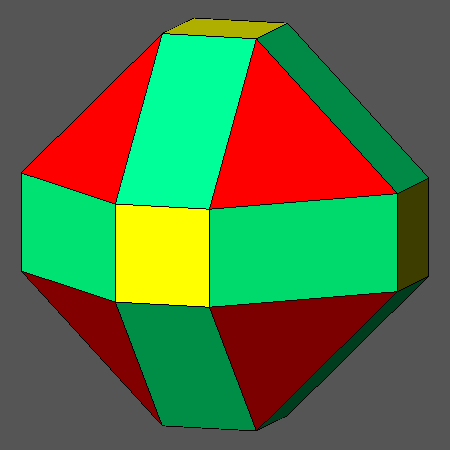When the value of the ratio dcube/doctahedron
of the central distances is equal to √3/2,
from the combination of cube and octahedron one obtains the compound polyhedron
shown in Fig.2c, in which the twelve edges of cube intercept midway the twelve edges of octahedra; left unchanged the ratio
dcube/doctahedron, these points are also the vertices of the cuboctahedron (Fig.2a),
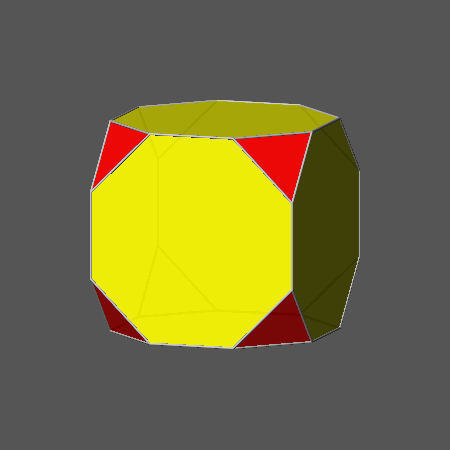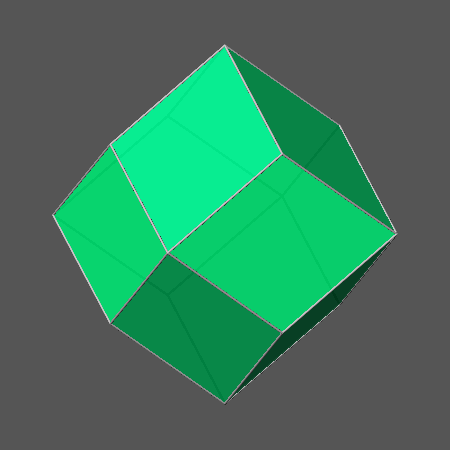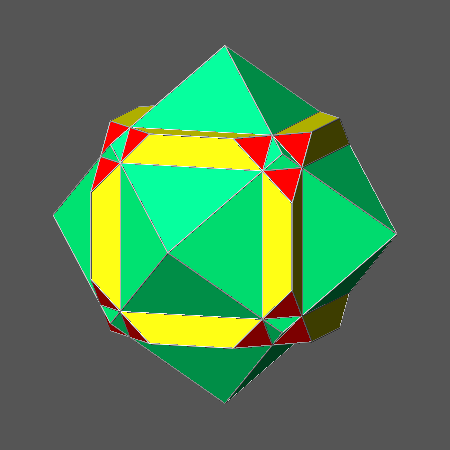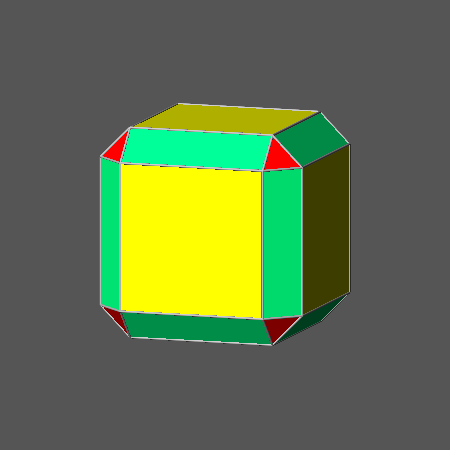
Archimedean polyhedron resulting from the intersection of cube and octahedron, made of six square faces of cube and eight equilateral triangular faces of octahedron.
The animated sequence showing both the cuboctahedron and the related compound polyhedron is reported in Fig.2b.
If one applies the formula √2dcube+√6doctahedron=
4dRD,
relative to the central distances dcube, doctahedron and dRD
of the single forms belonging to each vertex-transitive polyhedron dual of a deltoid-icositetrahedron,
to the specific case of the solid obtained truncating a cuboctahedron by its dual rhomb-dodecahedron, from the value of the ratio
dcube/doctahedron= √3/2
it follows that dRD/doctahedron= 3√6/8
and dRD/dcube= 3√2/4.
Taking into account that a rhomb-dodecahedron is tangent to the vertices of a cuboctahedron, in which
dcube= √2/2 and
doctahedron= √2/√3,
when its faces are at the central distance dRD= 1,
such value of dRD must decrease from 1 to 3/4 in order to obtain, as result of the truncation of
CO by RD, a vertex-transitive polyhedron, dual of the deltoid-icositetrahedron {211},
in which each rectangular face of rhomb-dodecahedron shares its sides with two triangular faces of octahedron and two square faces of cube:
√2 is the ratio between the lengths of the sides of the square and triangular faces.
The animated sequence describing such truncation process is reported in Fig.3b, whereas the convex vertex-transitive polyhedron and the corresponding compound polyhedron
are shown in Fig.3a and Fig.3c, respectively.
At this point, one can take into consideration the truncation of the vertex-transitive polyhedron by its dual, the deltoid-icositetrahedron {211}.
The sequence reporting the most significant steps of the complete truncation process is reported in the Appendix (Fig.22a), together with the sequence of the respective duals
(Fig.22b).
In particular, the step leading to a solid with triangular faces of octahedron is described in the animated sequence of Fig.4b;
the convex polyhedron resulting from the truncation and the relative compound polyhedron are shown in Fig.4a and Fig.4c, respectively.
Fig.5a reports the convex polyhedron dual of the solid shown in Fig.4a: it consists in the intersection of the hexakis-octahedron {421} with the triakis-octahedron {332};
the corresponding compound polyhedron is shown in Fig.5c whereas Fig.5b consists in the animated sequence
reporting the correlated convex and compound polyhedra, together with the single forms {421} and {332}.
 |
 |
 |
Fig.2a) Archimedean cuboctahedron, made of six square and eight triangular faces, resulting when the value of the ratio
dcube/doctahedron is equal to √3/2 |
Fig.2b) Animated image showing the correlation between cuboctahedron
and the corresponding compound polyhedron consisting in the combination
of cube and octahedron, when dcube/doctahedron= √3/2 |
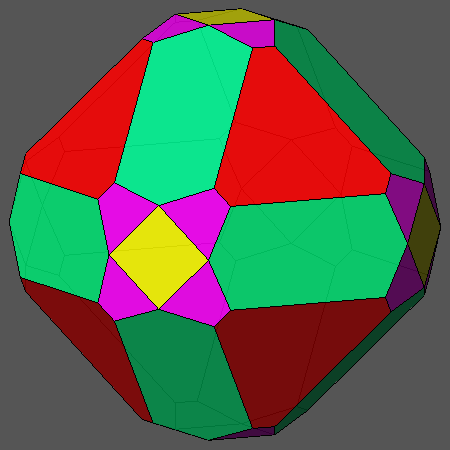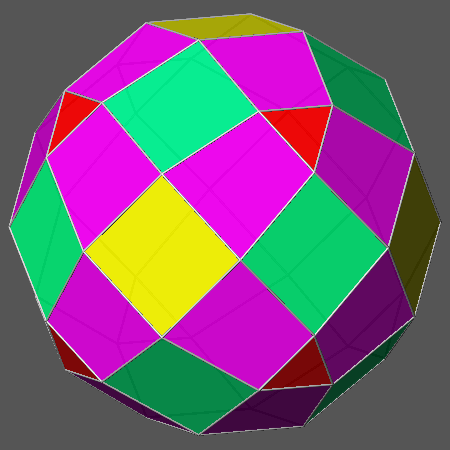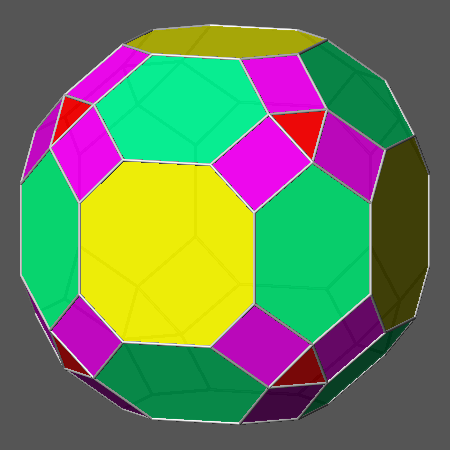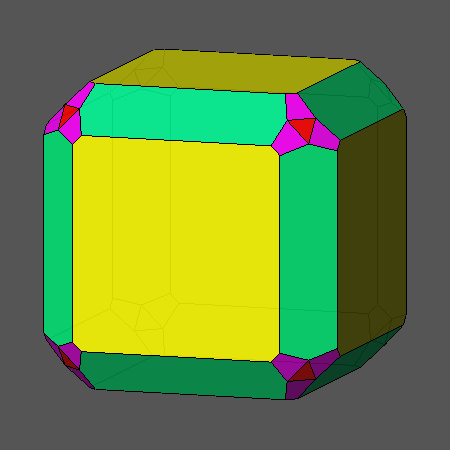
Fig.2c) Compound polyhedron, made of a cube and an octahedron,
resulting when
dcube/doctahedron= √3/2 |
_intersection_(RD_&CO_).png)
|
 |
_scaled7.png)
|
|
Fig.3a) Vertex-transitive polyhedron, dual of the deltoid icositetrahedron {211} obtained truncating a cuboctahedron
(in which dcube= √2/2
and doctahedron= √2/√3)
by its dual rhomb-dodecahedron, whose faces are at a central distance dRD= 3/4 |
Fig.3b) Animated sequence showing the derivation of:
the vertex-transitive polyhedron, shown in Fig.3a, from the intersection of a cuboctahedron with a rhomb-dodecahedron
the compound polyhedron, shown in Fig.3c, from the combination of a cuboctahedron with a rhomb-dodecahedron |
Fig.3c) Compound polyhedron consisting in the combination of a cuboctahedron with a rhomb-dodecahedron, whose faces are at a central distance dRD= 3/4 |
_intersection_(CO&RD)&dual_211.png) |
&211).gif) |
&211).png) |
Fig.4a) Convex polyhedron with triangular faces of octahedron resulting from the intersection of the vertex-transitive polyhedron reported in
Fig.3a with its dual, the deltoid-icositetrahedron {211} |
Fig.4b)
Animated sequence correlating the convex and compound polyhedra which result, respectively, from the intersection and combination of the solid reported in
Fig.3a with its dual, the deltoid-icositetrahedron {211} |
Fig.4c) Compound polyhedron resulting from the combination of the solid reported in Fig.3a
with its dual, the deltoid-icositetrahedron {211} |
 |
_new.gif) |
.png) |
Fig.5a) Dual of the solid reported in Fig.4a: it consists in the intersection of the hexakis-octahedron {421}
with the triakis-octahedron {332} |
Fig.5b) Animated sequence correlating the convex polyhedron shown in Fig.5a
and the compound polyhedron shown in Fig.5c
and including also the two single forms hexakis-octahedron {421} and triakis-octahedron {332} |
Fig.5c) Compound polyhedron made of the combination of the single forms hexakis-octahedron {421} and triakis-octahedron {332} |
Solids derived from the Archimedean truncated octahedron
When the value of the ratio dcube/doctahedron is included in the range
√3/2< dcube/doctahedron<√3,
the intersection of cube and octahedron gives rise to a truncated octahedron, consisting of square faces of cube and hexagonal faces of octahedron,
mostly non-regular polygons.
Relatively to whichever truncated octahedron in which the central distance of the face of octahedron is
doctahedron= √2/√3, a central distance dRD= 1 of the
faces of a rhomb-dodecahedron implies, irrespective of the value of dcube,
the tangency of all the faces of rhomb-dodecahedron to the twelve edges shared
by as many couples of faces of octahedron.
By inserting the value
doctahedron= √2/√3
in the formula
√2dcube+√6doctahedron=
4dRD,
relative to the distances of the single forms in each vertex-transitive polyhedron dual of a deltoid-icositetrahedron, one
can infer that the value of dRD must decrease from 1
to (√2dcube+2)/4
(with the central distance of the cube varying in the range:
√2/2< dcube<√2),
in order to obtain, from the intersection of each truncated octahedron with a rhomb-dodecahedron, a solid dual of a deltoid-icositetrahedron.
When the ratio dcube/doctahedron
increases from √3/2, value characterizing the cuboctahedron,
to its reciprocal 2/√3, the intersection of cube and octahedron generates another semiregular polyhedron made of six square and eight regular hexagonal faces, the
Archimedean truncated octahedron AtO.
It is shown in the animated sequence of Fig.6b together with a) a rhomb-dodecahedron,
b) a compound polyhedron made just of the combination of AtO and a rhomb-dodecahedron, and
c) the corresponding vertex-transitive convex polyhedron made of square, triangular and rectangular faces,
dual of the deltoid-icositetrahedron with indices {411}, obtained intersecting AtO with a rhomb-dodecahedron: it follows that, assigned the values
doctahedron= √2/√3
and consequently dcube= 2√2/3 to the central distances of octahedron and cube
in AtO, the faces of rhomb-dodecahedron in the dual of the deltoid-icositetrahedron {411} are at a central distance dRD
= 5/6; furhermore, relatively to this polyhedron, √2/3
is the ratio between the lengths of the sides that the square and triangular faces share with a rectangular face of rhomb-dodecahedron.
The vertex-transitive convex polyhedron dual of {411} and the related compound polyhedron are shown in Fig.6a and Fig.6c, respectively.
The intersection of the deltoid-icositetrahedron {411} with its dual can lead to a convex polyhedron (shown in Fig.7a)
in which the faces of cube are square; the corresponding compound polyhedron is shown in Fig.7c.
The couple of dual polyhedra and the results of their intersection and combination are reported in the animated sequence of Fig.7b.
Other polyhedra obtained at different steps of the intersection process between {411} and its dual are reported, together with their duals,
in Fig.23a and Fig.23b of the Appendix.
The dual of the solid reported in
Fig.7a consists in the intersection of the hexakis-octahedron {11 4 3} with the tetrakis-hexahedron {410};
it is shown in Fig.8a, the corresponding compound polyhedron in Fig.8c
and the animated sequence correlating the convex and compound polyhedra in Fig.8b.
 |
 |
 |
Fig.6a) Convex vertex-transitive polyhedron derived from the intersection of an Archimedean truncated octahedron AtO, in which
dcube= 2√2/3
and doctahedron= √2/√3,
with a rhomb-dodecahedron, whose faces are at a central distance dRD= 5/6 |
Fig.6b) Animated sequence showing the vertex-transitive convex polyhedron
shown in Fig.6a and the compound polyhedron shown in Fig.6c |
Fig.6c) Compound polyhedron consisting in the combination of an Archimedean truncated octahedron AtO, in which
dcube= 2√2/3
and doctahedron= √2/√3,
with a rhomb-dodecahedron whose faces are at a central distance dRD= 5/6 |
 |
 |
 |
Fig.7a)
Convex polyhedron; with square faces of cube resulting from the intersection of the polyhedron
reported in Fig.6a
with its dual, the deltoid-icositetrahedron {411} |
Fig.7b)
Animated sequence correlating the convex and compound polyhedra which result, respectively, from the intersection and combination of the solid reported in
Fig.6a with its dual, the deltoid-icositetrahedron {411} |
Fig.7c)
Compound polyhedron resulting from the combination of the solid reported in Fig.6a with its dual,
the deltoid-icositetrahedron {411} |
_.png) |
_new.gif) |
_compound_.png) |
Fig.8a)
Convex polyhedron dual of the solid reported in Fig.7a,
consisting in the intersection of two single forms, the hexakis-octahedron {11 4 3} and the tetrakis-hexahedron {410} |
Fig.8b)
Animated sequence correlating the convex polyhedron shown in Fig.8a
and the compound polyhedron shown in Fig.8c,
and including also the single forms:
hexakis-octahedron {11 4 3} and tetrakis-hexahedron {410} |
Fig.8c)
Compound polyhedron made of the combination of two single forms, the hexakis-octahedron {11 4 3} and the tetrakis-hexahedron {410} |
Solids derived from the Archimedean truncated cube
When the value of the ratio dcube/doctahedron
is included in the range
√3/3 < dcube/doctahedron< √3/2,
the intersection of cube and octahedron gives rise to a truncated cube,
consisting of equilateral triangular faces of octahedron and octagonal faces of cube, mostly non-regular polygons.
Relatively to whichever truncated cube in which the central distance of the faces of cube is
dcube= √2/2,
a central distance dRD = 1 of the faces of rhomb-dodecahedron implies,
irrespective of the value of doctahedron,
the tangency of the faces of rhomb-dodecahedron to all the twelve edges shared by as many couples of faces of cube.
By inserting the value dcube= √2/2
in the formula correlating the central distances in vertex-transitive polyhedra dual of deltoid-icositetrahedra,
one can infer that the value of dRD
must decrease from 1 to (1+√6doctahedron)/4
(with the central distance of the octahedron varying in the range:
√2/√3
< doctahedron<√3/√2),
in order to obtain, from the intersection of each truncated cube with a rhomb-dodecahedron, a solid dual of a deltoid-icositetrahedron.
When the value of the ratio dcube/doctahedron
becomes equal to √3/(√2+1),
the intersection of cube and octahedron generates another semiregular solid made of six regular octagons and eight equilateral triangular faces,
the Archimedean truncated cube AtC.
It is shown in the animated sequence of Fig.9b together with a) a rhomb-dodecahedron, b)
a compound polyhedron, consisting in the combination of AtC with the truncating rhomb-dodecahedron,
and c) the corresponding vertex-transitive convex polyhedron made of square, triangular and rectangular faces,
dual of the deltoid-icositetrahedron with indices {√211},
obtained intersecting the Archimedean truncated cube with a rhomb-dodecahedron.
In this vertex-transitive polyhedron (where 2+√2 is the ratio of the lengths of the sides
of the square and triangular faces) the faces of rhomb-dodecahedron are at a central distance
dRD= (2+√2)/4,
accordingly to the assignment of the value dcube= √2/2,
and consequently doctahedron= (√2+1)/√6,
to the central distances of cube and octahedron in the Archimedean truncated cube from which it derives.
The vertex-transitive convex polyhedron dual of {√2 1 1}
and the related compound polyhedron are shown separately in Fig.9a and Fig.9c, respectively.
The intersection of the deltoid-icositetrahedron {√2 1 1} with its dual
can lead to a convex polyhedron (shown in Fig.10a) in which the faces of octahedron are triangular
(other polyhedra obtained at different steps of the intersection process are reported, together with their duals, in Fig.24a and Fig.24b of the Appendix)
and the corresponding compound polyhedron is shown in Fig.10c.
The couple of dual polyhedra and the results of their combination are reported in the animated sequence of Fig.10b.
The dual of the solid reported in Fig.10a consists in the intersection of the hexakis-octahedron
{2√2 2√2-1 2}
with the triakis-octahedron {√2+1 √2+1 2}:
it is shown in Fig.11a, the corresponding compound polyhedron in Fig.11c,
and the animated sequence correlating the convex- and compound polyhedra in Fig.11b.
 |
 |
.png) |
Fig.9a)
Vertex-transitive polyhedron obtained from the intersection of an Archimedean truncated cube AtC, in which the central distances of the faces are
dcube= √2/2
and doctahedron= √2+1)/√6,
with a rhomb-dodecahedron, whose faces are at a central distance dRD= (2+√2)/4 |
Fig.9b)
Animated sequence correlating the convex- and compound polyhedra derived from the intersection and combination of AtC
with a rhomb-dodecahedron whose faces are at a central distance dRD= (2+√2)/4 |
Fig.9c)
Compound polyhedron consisting in the combination with AtC of a rhomb-dodecahedron whose faces are at a central distance
dRD= (2+√2)/4 |
 |
.gif) |
&dual).png) |
Fig.10a)
Convex polyhedron with triangular faces of octahedron resulting from the intersection of the polyhedron reported in
Fig.9a with its dual,
the deltoid-icositetrahedron {√2 1 1} |
Fig.10b)
Animated sequence correlating the convex and compound polyhedra which result, respectively, from the intersection and combination of the solid reported in
Fig.9a with its dual, the deltoid-icositetrahedron
{√2 1 1} |
Fig.10c)
Compound polyhedron resulting from the combination of the polyhedron reported in Fig.9a
with its dual, the deltoid-icositetrahedron {√2 1 1} |
_new.png) |
_new.gif) |
_compound.png) |
Fig.11a)
Convex polyhedron dual of the solid reported in Fig.10a
and consisting in the intersection of two single forms,
the hexakis-octahedron {2√2 2√2-1 2}
and the triakis-octahedron {√2+1 √2+1 2} |
Fig.11b)
Animated sequence correlating the convex polyhedron shown in Fig.11a
and the compound polyhedron shown in Fig.11c,
and including also the two single forms:
hexakis-octahedron {2√2 2√2-1 2}
and triakis-octahedron {√2+1 √2+1 2} |
Fig.11c)
Compound polyhedron made of the combination of two single forms,
the hexakis-octahedron {2√2 2√2-1 2}
and the triakis-octahedron {√2+1 √2+1 2}
|
Solids derived from the Archimedean truncated cuboctahedron
As stated in the introduction, the intermediate steps of the truncation
process by a rhomb-dodecahedron of whichever truncated octahedron lead to a continuous series of vertex-transitive polyhedra, dual of hexakis-octahedra:
in correspondence to each ratio doctahedron/dcube,
the resulting series of duals of hexakis-octahedra
is characterized by ratios dRD/dcube included in the following range:
(√2+√6doctahedron/dcube)/4
< dRD/dcube
< (√3/√2)(doctahedron/dcube).
When the value of the ratio
doctahedron/dcube
is set to √3/(3-√2),
the range becomes: (8√2+3)/14
< dRD/dcube
< (9√2+6)/14
and in particular, a noteworthy result is obtained when
dRD/dcube= (5√2+1)/7
(and consequently dRD/doctahedron
= (2√2-1)/√3):
indeed the resulting vertex-transitive polyhedron is the Archimedean truncated cuboctahedron (AtCO) shown in Fig.12b,
made of square faces of rhomb-dodecahedron, regular hexagonal faces of octahedron and regular octagonal faces of cube (as already pointed out
[1], its name is rather misleading, since it cannot be obtained
from the direct truncation of a cuboctahedron; therefore sometimes the name great rhombicuboctahedron is alternatively used).
The dual of AtCO is the Catalan hexakis-octahedron
{2√2+1 √2+1 1}, archetype of all the hexakis-octahedra
dual of vertex-transitive solids obtained from the intersection with a rhomb-dodecahedron of whichever truncated octahedron or truncated cube.
The animated sequence reported in Fig.12b includes AtCO and two related compound polyhedra,
obtained starting either from the single forms, cube and octahedron, or from their intersection, shown in Fig.12a
together with the corresponding compound polyhedron, generated from the combination of cube and octahedron.
A further reduction of the ratio dRD/dcube
from the value relative to AtCO, (5√2+1)/7,
to (8√2+3)/14 leads to a vertex-transitive convex polyhedron, dual of the deltoid-icositetrahedron
{3√2-2 1 1},
made of square, triangular and rectangular faces: the ratio between the lengths of the sides that the square and triangular faces share with the rectangular faces is
(2+√2)/3.
If one inserts in dRD/dcube=
(8√2+3)/14 the value
dcube= (5√2-1)/7
characterizing also AtCO when dRD=1,
the resulting value of dRD in the dual of the deltoid-icositetrahedron
{3√2-2 1 1}
becomes dRD= 1-[(3-√2)/14].
The animated sequence reported in Fig.12c includes, together with this vertex-transitive convex polyhedron,
two compound polyhedra derived from the combination of the rhomb-dodecahedron with each of the two solids shown in Fig.12a.
One can realize that, relatively to the compound polyhedron resulting from the combination of the three single forms,
its exterior shape does not include the rhomb-dodecahedron, whose faces result to be internally tangent to the compound polyhedron, made of the only cube and octahedron;
therefore it is identical to the compound polyhedron shown in Fig.12a.
The intersection of the deltoid-icositetrahedron {3√2-2 1 1}
with its dual vertex-transitive polyhedron can lead to a convex polyhedron (shown in Fig.13a), in which the faces of octahedron are triangular,
whereas the corresponding compound polyhedron is shown in Fig.13c
(also in this case, other polyhedra obtained at different steps of the intersection process between the deltoid-icositetrahedron
{3√2-2 1 1} and its dual are reported, together with their duals, in Fig.25a and Fig.25b of the Appendix).
The couple of dual polyhedra and the results of their combination are reported in the animated sequence of Fig.13b.
The dual of the solid reported in Fig.13a consists in the intersection of the hexakis-octahedron
{10√2+12 4√2+6 4√2-3}
with the triakis-octahedron {3√2-1 3√2-1 2}:
it is shown in Fig.14a, the corresponding compound polyhedron is shown in Fig.14c,
whereas the animated sequence correlating the convex and compound polyhedra is shown in Fig.14b.
 |
 |
 |
|
Fig.12a)
Compound polyhedron and relative non-Archimedean convex polyhedron resulting from the intersection of a cube and an octahedron
when the value of the ratio doctahedron/dcube
is equal to √3/(3-√2),
as in Archimedean truncated cuboctahedron |
Fig.12b)
Animated sequence showing the Archimedean truncated cuboctahedron and two related compound polyhedra resulting from the combination
with a rhomb-dodecahedron of either the two single forms cube and octahedron or their intersection shown in Fig.12a,
when, fixed the ratio
doctahedron/dcube= √3/(3-√2),
dRD/dcube becomes equal to (5√2+1)/7 and consequently
dRD/doctahedron =
(2√2-1)/√3 |
Fig.12c)
Animated sequence showing, together with the vertex transitive convex polyhedron, dual of the deltoid-icositetrahedron
{3√2-2 1 1}, obtained by decreasing the value of dRD in AtCO,
two related compound polyhedra resulting from the combination with a rhomb-dodecahedron, of either the single forms cube and octahedron or their intersection
shown in Fig.12a |
 |
.gif) |
 |
Fig.13a)
Convex polyhedron, including triangular faces of octahedron, which results from the intersection
with the deltoid-icositetrahedron having indices {3√2-2 1 1}
of its dual, the vertex-transitive polyhedron obtained by decreasing the central distance of the rhomb-dodecahedron in AtCO |
Fig.13b)
Animated sequence correlating the solids reported in Fig.13a and Fig.13c,
resulting from the intersection and combination of the deltoid-icositetrahedron
{3√2-2 1 1} with its vertex-transitive dual |
Fig.13c)
Compound polyhedron resulting from the combination of the deltoid-icositetrahedron {3√2-2 1 1}
with its dual, the vertex-transitive polyhedron obtained by decreasing the central distance of the rhomb-dodecahedron in AtCO |
_scaled04.png) |
_new.gif) |
_04.png) |
Fig.14a)
Convex polyhedron dual of the solid reported in Fig.13a:
it consists in the intersection of two single forms, the hexakis-octahedron
{10√2+12 4√2+6 4√2-3}
and the triakis-octahedron {3√2-1 3√2-1 2} |
Fig.14b)
Animated sequence correlating the convex polyhedron shown in Fig.14a
and the compound polyhedron shown in Fig.14c,
and including also two single forms, the hexakis-octahedron
{10√2+12 4√2+6 4√2-3}
and the triakis-octahedron {3√2-1 3√2-1 2} |
Fig.14c)
Compound polyhedron made of the combination of two forms, the hexakis-octahedron
{10√2+12 4√2+6 4√2-3}
and the triakis-octahedron {3√2-1 3√2-1 2} |
Solids derived from rhombicuboctahedron
Another noteworthy combination of a cube with an octahedron is obtained when the value of the ratio
dcube/doctahedron
is equal to √3/(2√2-1):
the resulting compound polyhedron is shown in Fig.15a together with the corresponding convex polyhedron,
a truncated octahedron slightly different from the one, shown in Fig.12a, derived from AtCO.
After the usual series of vertex-transitive polyhedra, dual of hexakis-octahedra,
obtained from the intersection of this truncated octahedron with a rhomb-dodecahedron,
a further decrease of dRD leads to a peculiar polyhedron when its value
coincides with the value of dcube and
consequently also dRD/doctahedron= √3/(2√2-1);
such polyhedron, dual of the Catalan deltoid-icositetrahedron {√2+1
1 1}, is the Archimedean rhombicuboctahedron (RCO), made of equilateral triangular faces of octahedron and square faces of both cube and rhomb-dodecahedron
(it is alternatively called small rhombicuboctahedron, in analogy with the name great rhombicuboctahedron given to AtCO).
It is interesting to note that the values of the ratio
dRD/doctahedron
in RCO and AtCO are reciprocal: √3/(2√2-1)
and (2√2-1)/√3, respectively.
The animated sequence of Fig.15b describes the derivation of both RCO and a related compound polyhedron from the intersection and combination
with a rhomb-dodecahedron of the truncated octahedron shown in Fig.15a.
In Fig.15c another animated sequence shows RCO and a further related compound polyhedron which derives from the combination
with a rhomb-dodecahedron of the compound polyhedron shown in Fig.15a.
One can verify that, relatively to the compound polyhedron resulting from the combination of the three single forms: cube, octahedron and rhomb-dodecahedron,
also in this case its exterior shape does not include the rhomb-dodecahedron, whose faces result to be internally tangent to the compound polyhedron
made of the only cube and octahedron, therefore identical to the compound polyhedron shown in Fig.15a.
In general this feature characterizes each compound polyhedron, related to the dual of a deltoid-icositetrahedron, resulting from the combination of the three single forms.
The intersection of RCO with the dual Catalan deltoid-icositetrahedron {√2+1
1 1} can lead to a convex polyhedron with trapezoidal faces of deltoid-icositetrahedron, in which the faces of cube and rhomb-dodecahedron are still square,
and the faces of octahedron are still triangular but all are differently oriented in respect to RCO:
it is shown in Fig.16a and the corresponding compound polyhedron is shown in Fig.16c.
The couple of dual polyhedra and the results of their combination are reported in the animated sequence of Fig.16b.
(Also in case of the intersection between RCO and its dual deltoid-icositetrahedron, other polyhedra obtained at different steps
of the intersection process are reported, together with their duals, in Fig.26a and Fig.26b of the Appendix).
The dual of the solid reported in Fig.16a consists in the intersection of the triakis-octahedron
{2-√2 1 1}
with the tetrakis-hexahedron {√2+1 1 0},
having the same central distance; it is shown in Fig.17a and the corresponding compound polyhedron is shown in Fig.17c.
The animated sequence correlating the convex and compound polyhedra is reported in Fig.17b.
The convex polyhedron shown in Fig.18a can be obtained from the intersection of the dual couple of polyhedra reported in Fig.16a and Fig.17a:
the related compound polyhedron is shown in Fig.18c and the animated sequence correlating the convex and compound polyhedra in Fig.18b.
The dual of the polyhedron shown in Fig.18a consists in the intersection of three hexakisoctahedra,
having the same central distance, and a deltoid-cositetrahedron.
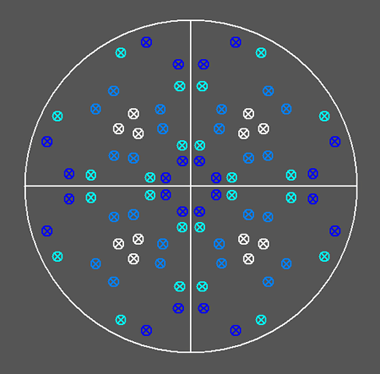
Fig.19a shows an orthographic view of this polyhedron, whereas the view along the vertical direction [001] and the corresponding stereonet projection
of the faces are reported in Fig.19c and Fig.19b, respectively.
In detail, the animated sequence of Fig.20a includes the following single forms:
a deltoid-icositetrahedron with indices
{2 3-√2 3-√2}
three hexakis-octahedra with indices:
{4(√2+1) 3 1},
{7√2+8 √2+8 2},
{5√2+8 3√2+8 6}
whereas the results of their progressive intersection can be viewed in the animated sequence of Fig.20b.
 |
 |
 |
|
Fig.15a)
Compound polyhedron, made of a cube and an octahedron, and the related convex polyhedron resulting from their intersection when the value of the ratio
dcube/doctahedron
is √3/(2√2-1)
as in the Archimedean rhombicuboctahedron RCO |
Fig.15b)
Animated sequence showing the derivation of RCO and the related compound polyhedron from the intersection and combination
with a rhomb-dodecahedron, whose faces are at the central distance dRD= 1,
of the convex polyhedron shown in Fig.15a, when
doctahedron= (2√2-1)/√3
and dcube= 1 |
Fig.15c)
Animated sequence showing RCO and the derivation of the related compound polyhedron, made of the single forms,
from the combination with a rhomb-dodecahedron of the compound polyhedron shown in Fig.15a |
 |
 |
 |
Fig.16a)
Convex polyhedron (inscribable in a sphere as the duals of all the deltoid-icositetrahedra) resulting from the intersection
of the Archimedean rhombicuboctahedron with its dual, the Catalan deltoid-icositetrahedron
{√2+1 1 1} |
Fig.16b)
Animated sequence showing the combination and intersection of the Archimedean rhombicuboctahedron with its dual,
the Catalan deltoid-icositetrahedron {√2+1 1 1}, resulting in the convex polyhedron
shown in Fig.16a and the related compound polyhedron shown in Fig.16c |
Fig.16c)
Compound polyhedron resulting from the combination of the Archimedean rhombicuboctahedron with its dual, the Catalan deltoid-icositetrahedron
{√2+1 1 1} |
_scaled.png) |
_new.gif) |
_scaled.png)
|
Fig.17a)
Dual of the convex polyhedron reported in Fig.16a and consisting in the intersection
of two single forms, the triakis-octahedron {2-√2 1 1}
and the tetrakis-hexahedron {√2+1 1 0} |
Fig.17b)
Animated sequence correlating the convex polyhedron shown in
Fig.17a and the compound polyhedron shown in
Fig.17c; also the single forms
triakis-octahedron {2-√2 1 1}
and tetrakis-hexahedron {√2+1 1 0} are included |
Fig.17c)
Compound polyhedron made of the combination of the triakis-octahedron {2-√2 1 1}
and the tetrakis-hexahedron {√2+1 1 0}
|
&dual_(RCO&dual)_scaled.png) |
&(dual_(RCO&dual))_.gif) |
&(dual_(RCO&dual))_.png) |
|
Fig.18a)
Convex polyhedron deriving from the intersection of the solid shown in Fig.16a
and its dual shown in Fig.17a |
Fig.18b)
Animated sequence correlating the convex polyhedron shown in Fig.18a
and the compound polyhedron shown in Fig.18c |
Fig.18c)
Compound polyhedron corresponding to the convex polyhedron shown in Fig.18a |
 |
 |
 |
|
Fig.19a)
Convex polyhedron dual of the solid reported in Fig.18a: it includes
three hexakis-octahedra and a deltoid-icositetrahedron. |
Fig.19b)
Stereonet projection of the 168 faces belonging to the four forms of the polyhedron shown in the side views. |
Fig.19c)
View along the vertical direction [001] of the polyhedron reported in Fig.19a |
 |
 |
|
Fig.20a)
Animated sequence including the three hexakis-octahedra and the deltoid-icositetrahedron, whose intersection generates the solid
shown in Fig.19a |
Fig.20b)
Sequential steps of the intersection processes relative to the three hexakis-octahedra and the deltoid-icositetrahedron, leading to the solid shown in
Fig.19a |
The main features relative to the compound polyhedra derived from the different Archimedean polyhedra are
summarized in Fig.21, consisting of four animated sequences.
 |
 |
|
Fig.21a)
Animated sequence consisting of the compound polyhedra related to the five Archimedean cubic polyhedra ordered as in
Fig.1a |
Fig.21b)
Double animated sequence of the compound polyhedra related to the five vertex-transitive duals of deltoid-icositetrahedra:
the second one in each sequence derives from RCO, whereas the others derive from the truncation of the
remaining Archimedean polyhedra with m3m symmetry. |
 |
 |
Fig.21c)
Animated sequence consisting of the compound polyhedra related to the polyhedra shown in Fig.1c,
derived from the intersection of each deltoid-icositetrahedron with its vertex-transitive
dual.
|
Fig.21d)
Animated sequence consisting of the compound polyhedra related to the polyhedra shown in Fig.1d |
APPENDIX
Significant steps of the progressive truncation by
the deltoid-icositetrahedron {211} of its vertex-transitive dual, in turn
derived from the intersection of a cuboctahedron with a rhomb-dodecahedron
A result of the truncation by the deltoid-icositetrahedron {211} of its vertex-transitive dual,
in turn derived from the intersection of a cuboctahedron with its dual rhomb-dodecahedron, is the polyhedron, shown in Fig.4a, in which the faces of octahedron
have the shape of equilateral triangles.
Fig.22a consists in an animated sequence including also the polyhedra obtained
at other significant steps of the entire truncation process by the deltoid-icositetrahedron {211};
the corresponding duals are reported in Fig.22b.
Starting from the vertex-transitive dual of the deltoid-icositetrahedron {211}, the subsequent steps include:
- a polyhedron in which the faces of octahedron are regular hexagons: its dual consists in the intersection of the two hexakis-octahedra {543} and {632}
- a polyhedron in which the faces of octahedron are equilateral triangles: its dual consists in the intersection of the triakis-octahedron {332}
with the hexakis-octahedron {421}
- a polyhedron in which the faces of cube are regular octagons: its dual consists in the intersection of the two triakis-octahedra
{1 1 2√2-2} and {3 3 2√2-1}
with the hexakis-octahedron {2 1 √2-1}
- a polyhedron in which the faces of octahedron are vanisheded: its dual consists in the intersection
with an octahedron
of the triakis-octahedron {995} and the hexakis-octahedron {631}
- a polyhedron in which the faces of cube are square and the faces of rhomb-dodecahedron are rhombic
(ratio of the diagonals =√2):
its dual consists in the intersection with an octahedron of the triakis-octahedron {331} and the tetrakis-hexahedron {210}
- a polyhedron in which also the faces of rhomb-dodecahedron are vanished: its dual consists in the intersection of an octahedron
and a rhomb-dodecahedron with the tetrakis-hexahedron {410}
- a polyhedron consisting of the only deltoid-icositetrahedron {211}, after the vanishing of the faces of the cube, too:
its vertex-transitive dual consists obviously in the intersection of cube, octahedron and rhomb-dodecahedron
&dual211).gif) |
&dual)).gif) |
|
Fig.22a)
Animated sequence consisting of the significant steps of the progressive truncation, by the deltoid-icositetrahedron {211}, of its vertex-transitive dual,
in turn obtained from the truncation of a cuboctahedron by a rhomb-dodecahedron |
Fig.22b)
Animated sequence including the duals of each polyhedron belonging to the sequence reported in Fig.22a |
Significant steps of the progressive truncation by the deltoid-icositetrahedron {411} of its vertex-transitive dual, in turn
derived from the intersection of AtO with a rhomb-dodecahedron
A result of the truncation by the deltoid-icositetrahedron {411} of its vertex-transitive dual, derived from the intersection of the Archimedean truncated octahedron AtO
with a rhomb-dodecahedron, is the polyhedron shown in Fig.7a, in which the faces of cube are square.
Fig.23a consists in an animated sequence including also the polyhedra obtained at other significant steps of the entire truncation process by the deltoid-icositetrahedron {411};
the corresponding duals are reported in Fig.23b.
Starting from the vertex-transitive dual of the deltoid-icositetrahedron {411}, the subsequent steps include:
- a polyhedron with regular octagonal faces of cube: its dual consists in the intersection of the
two hexakis-octahedra {4 1 √2-1}
and {10+√2 5-√2 3}
- a polyhedron with square faces of cube: its dual consists in the intersection with the tetrakis-hexahedron {410} of the hexakis-octahedron {11 4 3}
- a polyhedron in which the faces of cube are just vanished: its dual consists
in the intersection with a cube of the tetrakis-hexahedron {11 4 0} and the hexakis-octahedron {10 5 3}
- a polyhedron in which the faces of octahedron are regular hexagons: its dual
consists in the intersection with a cube of the tetrakis-hexahedron {210} and the hexakis-octahedron {321}
- a polyhedron in which the faces of octahedron are equilateral triangles and the face of rhomb-dodecahedron are rhombic
(ratio of the diagonals =√2/3): its dual
consists in the intersection with a cube of the tetrakis-hexahedron {5√2
+1 9-2√2 0} and the triakis-octahedron {552}
- a polyhedron in which also the faces of rhomb-dodecahedron are vanished: its dual consists in the intersection of the triakis-octahedron {13 13 10}
with a cube and a rhomb-dodecahedron
- a polyhedron consisting in the only deltoid-icositetrahedron {411}, due to the vanishing of the faces of octahedron, too.
 |
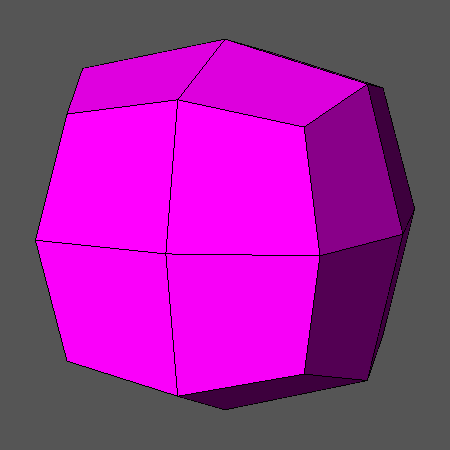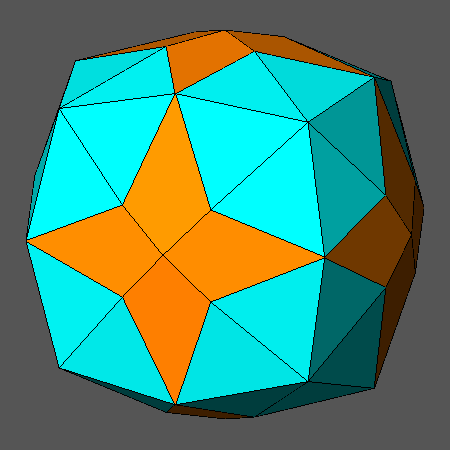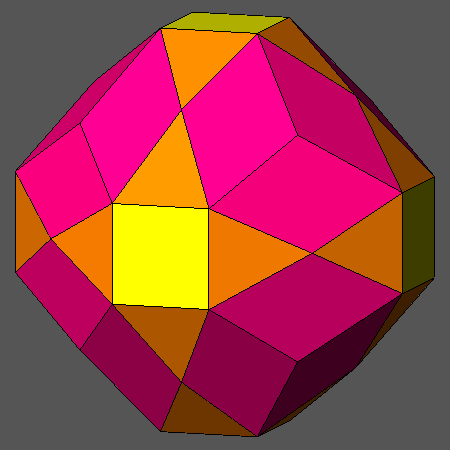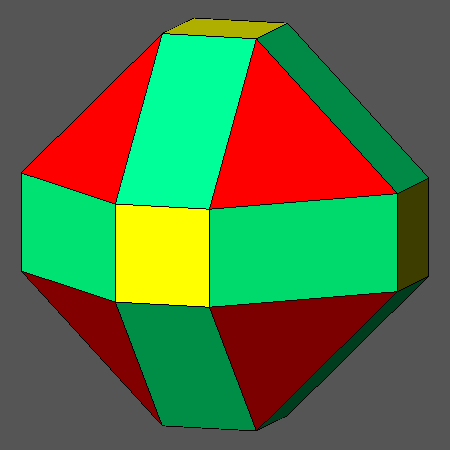 |
|
Fig.23a)
Animated sequence consisting of significant steps of the progressive truncation, by the {411} deltoid-icositetrahedron,
of its vertex-transitive dual, in turn resulting from the intersection of the Archimedean truncated octahedron
with a rhomb-dodecahedron |
Fig.23b)
Animated sequence including the duals of each polyhedron belonging to the sequence reported in Fig.23a |
Significant steps of the progressive truncation by the deltoid-icositetrahedron {√211}
of its vertex-transitive dual, in turn derived from the intersection of AtC with a rhomb-dodecahedron
A result of the truncation by the deltoid-icositetrahedron {√211}
of its vertex-transitive dual, derived from the intersection of the Archimedean truncated cube AtC with a rhomb-dodecahedron,
is the polyhedron shown in Fig.10a, in which the face of octahedron have the shape of equilateral triangles.
Fig.24a consists in an animated sequence including also the polyhedra obtained at other significant steps of the entire truncation process by the deltoid-icositetrahedron
{√211}; the corresponding duals are reported in Fig.24b.
Starting from the vertex-transitive dual of the deltoid-icositetrahedron {√211}, the subsequent steps include:
-
a polyhedron in which the faces of octahedron are regular hexagons: its dual consists in the intersection of the hexakis-octahedra
{3√2 3 2√2}
and {2√2+1 3 √2+2}
-
a polyhedron in which the faces of octahedron are equilateral triangles: its dual consists in the intersection of the hexakis-octahedron
{2√2 2√2-1 2}
with the triakis-octahedron {√2+1 √2+1 2}
-
a polyhedron in which the faces of octahedron are just vanished: its dual
consists in the intersection with an octahedron of the triakis-octahedron {3 3 √2+1}
and the hexakis-octahedron {3√2
3 4√2-3}
-
a polyhedron in which the faces of cube are regular octagons: its dual
consists in the intersection with an octahedron
of the triakis-octahedron {1 1 √2-1}
and the hexakis-octahedron {√2 1 √2-1}
-
a polyhedron in which the faces of cube are square and the faces of rhomb-dodecahedron
are rhombic (ratio of the diagonals =√2+2):
its dual consists in the intersection with an octahedron of the triakis-octahedron {1 1 10√2-7}
and the tetrakis-hexahedron {√2 1 0}
-
a polyhedron in which also the faces of rhomb-dodecahedron are vanished: its dual consists in the intersection of
an octahedron and a rhomb-dodecahedron
with the tetrakis-hexahedron {4 4-√2 0}
-
a polyhedron consisting in the only deltoid-icositetrahedron {√2 1 1},
due to the vanishing of the faces of cube, too
 |
 |
|
Fig.24a)
Animated sequence consisting of significant steps of the progressive truncation, by the deltoid-icositetrahedron
{√2 1 1}, of its vertex-transitive dual,
in turn resulting from the intersection of the Archimedean truncated cube with a rhomb-dodecahedron |
Fig.24b)
Animated sequence including the duals of each polyhedron belonging to the sequence reported in Fig.24a |
Significant steps of the progressive truncation, by the deltoid-icositetrahedron {3√2-2 1 1},
of its vertex-transitive dual, in turn obtained by decreasing the central distance of the faces of rhomb-dodecahedron in the Archimedean truncated cuboctahedron
A result of the truncation by the deltoid-icositetrahedron {3√2-2 1 1} of its vertex-transitive dual,
obtained by decreasing the central distance of the faces of rhomb-dodecahedron in the Archimedean truncated cuboctahedron, is the polyhedron shown in Fig.13a,
in which the face of octahedron have the shape of equilateral triangles.
Fig.25a consists in an animated sequence including also the polyhedra obtained at other significant steps of the entire truncation process by the deltoid-icositetrahedron
{3√2-2 1 1}; the corresponding duals are reported in Fig.25b.
Starting from the vertex-transitive dual of the deltoid-icositetrahedron {3√2-2 1 1}, the subsequent steps include:
-
a polyhedron in which the faces of octahedron are regular hexagons: its dual consists in the intersection of the hexakis-octahedra
{6√2 +10 3√2+4 4}
and {7 2√2+1 √2+4}
-
a polyhedron in which the faces of cube are regular octagons: its dual consists in the intersection of the hexakis-octahedra
{3√2-2 1 √2-1}
and {8√2-6 3 √2+3}
-
a polyhedron in which the faces of octahedron are equilateral triangles: its dual consists in the intersection of the hexakis-octahedron
{10√2+12 4√2+6 4√2-3}
and the triakis-octahedron {9√2+2 9√2+2 14}
-
a polyhedron with square faces of cube and rhombic faces of rhomb-dodecahedron (ratio of the
diagonals = (√2+2)/3): its dual consists in the intersection of
three polyhedra: the tetrakis-hexahedron {3√2-1 1 0} and two triakis-octahedra
with indices {7√2+9 7√2+9 9}
and {3√2-1 3√2-1 2}
-
a polyhedron in which the faces of octahedron are just vanished: its dual consists in the intersection with an octahedron of the triakis-octahedron
{2√2+5 2√2+5
5-√2} and two tetrakis-hexahedra, having indices
{5√2-1 4(4√2-5) 0}
and {4√2+1 5√2-4 0}
-
a polyhedron in which also the faces of rhomb-dodecahedron are vanished:
its dual consists in the intersection of an octahedron and a rhomb-dodecahedron
with the tetrakis-hexahedron {10√2+12
4√2-3 0}
-
a polyhedron consisting in the only deltoid-icositetrahedron {3√2-2 1 1},
due to the vanishing of the faces of cube, too.
 |
 |
|
Fig.25a)
Animated sequence consisting of significant steps of the progressive truncation by the deltoid-icositetrahedron
{3√2-2 1 1}
of its vertex-transitive dual, in turn obtained decreasing the central distance of the rhomb-dodecahedron in the Archimedean truncated cuboctahedron |
Fig.25b) Animated sequence including the duals of each polyhedron belonging to the sequence reported in
Fig.25a |
Significant steps of the progressive truncation of the Archimedean rhombicuboctahedron by the Catalan deltoid-icositetrahedron
{√2+1 1 1}
A result of the truncation of the Archimedean
rhombicuboctahedron RCO by its dual, the Catalan deltoid-icositetrahedron {√2+1 1 1},
is the polyhedron reported in Fig.16a, in which, in addition to the faces of deltoid-icositetrahedron having a trapezoidal shape,
the face of octahedron have the shape of equilateral triangles, whereas the faces of cube and rhomb-dodecahedron are both square.
Fig.26a consists in an animated sequence including the polyhedra obtained at other significant steps of the entire truncation process
of RCO by the deltoid-icositetrahedron {√2+1 1 1}; the corresponding duals are reported in Fig.26b.
Starting from RCO, the subsequent steps include:
-
a polyhedron in which the faces of cube and rhomb-dodecahedron are equi-sized regular octagons: its dual consists in the intersection of the hexakis-octahedra
{2 1 √2}
and {√2+1 1 √2-1}
-
a polyhedron in which the faces of octahedron are regular hexagons: its dual consists in the intersection of the hexakis-octahedra
{3(√2+1) 3 1}
and {2√2+3 3 √2+3}
-
a polyhedron in which the faces of octahedron are equilateral triangles whereas the equi-sized faces of cube and rhomb-dodecahedron
are square: its dual consists in the intersection of the triakis-octahedron {2-√2 1 1}
with the tetrakis-hexahedron {√2+1 1 0}
-
a polyhedron in which the faces of octahedron are vanished: its dual consists in the intersection
with an octahedron
of the triakis-octahedron {3 3 2(2-√2)} and two tetrakis-hexahedra, having indices
{3 2(√2-1) 0}
and {2√2+1 5-2√2 0}
-
a polyhedron consisting in the only deltoid-icositetrahedron {√2+1 1 1}, due to the simultaneous vanishing
of the faces of cube and rhomb-dodecahedron, too.
 |
 |
|
Fig.26a)
Animated sequence consisting of significant steps of the progressive truncation of the Archimedean rhombicuboctahedron by its dual,
the Catalan deltoid-icositetrahedron {√2+1 1 1} |
Fig.26b)
Animated sequence including the duals of the solid belonging to the sequence reported in Fig.26a |
The intersection with its dual of each polyhedron obtained at the intermediate steps of the truncation process of RCO by the Catalan deltoid-icositetrahedron
can generate, as shown in the animated sequence of Fig.27a, three other remarkable solids, in addition to the polyhedron reported in Fig.18a;
it must be pointed out that the shape of the regular polygons included in the four solids (octagons, hexagons, triangles and squares, in succession)
is the same shape of the regular polygons present in the polyhedra from which every resulting solid derives.
The duals of the solids shown in the sequence of Fig.27a are reported in the corresponding sequence of Fig.27b
and consist, in turn, in the intersection of:
three deltoid-icositetrahedra: {2√2+1 2 2},
{√2+2 1 1} and {3 2 2},
the triakis-octahedron {1 1 2-√2},
the tetrakis-hexahedron {1 √2-1 0}
and the hexakis-octahedron {2√2-1 1
2-√2}
the deltoid-icositetrahedron
{2(√2+1) 5√2-4
5√2-4},
the triakis-octahedron {1 1 2-√2},
the tetrakis-hexahedron {1 √2-1 0}
and three hexakis-octahedra:
{3(3√2+4) 3(√2+4)
10},
{11√2+12 √2+12 6}
and {6(√2+1) 5 3}
the deltoid-icositetrahedron {2 3-√2 3-√2} and
the three hexakis-octahedra: {4(√2+1) 3 1},
{7√2+8 √2+8 2}
and {5√2+8 3√2+8
6}, as already reported in the text
again a deltoid-icositetrahedron,
with indices {3 √2-1 √2-1} and three hexakis-octahedra,
with indices:
{7(√2+1) 15 15-4√2},
{7+11√2 15-4√2
7-4√2}
and {3+2√2 3+√2
1}
 |
 |
|
Fig.27a)
Animated sequence consisting of the solids obtained from the intersection with its dual of each polyhedron which derives from the progressive truncation of RCO by
the Catalan deltoid-icositetrahedron |
Fig.27b)
Animated sequence including the duals of the solid belonging to the sequence reported in Fig.27a |
Features of the solids obtained sequentially from the progressive truncation by deltoid-icositetrahedra of their duals related to Archimedean polyhedra
The order of appearance of regular polygonal faces in the different solids obtained from the progressive truncation, by deltoid-icositetrahedra,
of their duals derived from Archimedean polyhedra is summarized in Table 3,
together with the order of vanishing of the forms: cube, octahedron and rhomb-dodecahedron.
The dual couples of intersecting solids are listed in the same order in which they appear in Fig.1a, namely according to
decreasing values of the ratio dcube/doctahedron.
|
{411} and dual coming from AtO |
Catalan {√2+1 1 1} and RCO |
{3√2-2 1 1} and dual coming from AtCO |
{211} and dual coming from CO |
{√2 11} and dual coming from AtC |
| regular octagonal faces of cube |
regular octagonal faces of cube |
regular hexagonal faces of octahedron |
regular hexagonal faces of octahedron |
regular hexagonal faces of octahedron |
| square faces of cube |
regular hexagonal faces of octahedron |
regular octagonal faces of cube |
equilateral triangular faces of octahedron |
equilateral triangular faces of octahedron |
| vanishing of the faces of cube |
equilateral triangular faces of octahedron |
equilateral triangular face of octahedron |
regular octagonal faces of cube |
vanishing of the faces of octahedron |
and square faces of both
cube and rhomb-dodecahedron |
regular hexagonal faces
of octahedron |
vanishing of the faces of octahedron |
square faces of cube |
vanishing of the faces of octahedron |
regular octagonal faces of cube |
equilateral triangular faces
of octahedron |
vanishing of the faces of cube
and rhomb-dodecahedron |
vanishing of the faces of octahedron |
square faces of cube |
square faces of cube |
vanishing of the faces
of rhomb-dodecahedron |
|
vanishing of the faces
of rhomb-dodecahedron |
vanishing of the faces
of rhomb-dodecahedron |
vanishing of the faces
of rhomb-dodecahedron |
vanishing of the faces
of octahedron |
|
vanishing of the faces of cube |
vanishing of the faces of cube |
vanishing of the faces of cube |
Table 3
Series of dual solids with cubic or icosahedral symmetry and relative intersections
The last couple of animated sequences, reported in Fig.28a and Fig.28b, illustrates one more time the close analogies between the solids
with 4/m 3 2/m cubic
and 2/m 3 5 icosahedral symmetry.
Each of the two sequences consists of:
- the Archimedean rhombicuboctahedron (in which the faces of cube and rhomb-dodecahedron are equi-sized squares, whereas the faces of octahedron have the shape of equilateral triangles)
or
the Archimedean rhomb-icosidodecahedron (in which the faces of rhomb-triacontahedron are square,
the faces of dodecahedron are regular pentagons and the faces of icosahedron have the shape of equilateral triangles)
- the dual Catalan deltoid-icositetrahedron
or
the dual Catalan deltoid-hexecontahedron: the faces of both Catalan polyhedra have the shape of kites
- the intersection between the polyhedra reported in 1 and 2,
characterized by:
equilateral
triangular faces of octahedron and square faces of cube and rhomb-dodecahedron, whereas the faces of deltoid-icositetrahedron are trapezoidal
or equilateral triangular faces of icosahedron, regular pentagonal faces of dodecahedron
and square faces of rhomb-triacontahedron, whereas the faces of deltoid-hexecontahedron are trapezoidal
- the dual of the polyhedron reported in 3, consisting of:
a triakis-octahedron and a tetrakis-hexahedron
or a triakis-icosahedron and a pentakis-dodecahedron
- the intersection between the polyhedra reported in 3 and 4, including:
equilateral triangular faces of octahedron
or equilateral triangular faces of icosahedron
- the dual of the polyhedra reported in 5, consisting of:
a deltoid-icositetrahedron and three hexakis-octahedra
or a deltoid-hexacontahedron and three hexakis-icosahedra
 |
 |
|
Fig.28a) Series of dual polyhedra with
4/m 3 2/m cubic symmetry and relative intersections, all derived from the Archimedean rhombi-cuboctahedron |
Fig.28b) Series of duals with 2/m 3 5 icosahedral symmetry
and relative intersections, all derived from the Archimedean rhomb-icosidodecahedron: the analogies with the corresponding images
of the series in Fig.27a, taking into account the different symmetry, are evident. |
LINKS and REFERENCES
- L. ZEFIRO
Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra
Vismath, Vol.13, No.2, 2011, ISSN 2117-6888 (online)
- L. ZEFIRO
Regular shaped faces in solids with cubic symmetry derived from truncation processes by rhomb-dodecahedron or cube
Vismath, Vol.13, No.2, 2011, ISSN 2117-6888 (online)
- P. CROMWELL
Polyhedra
Cambridge University Press, 1997, ISBN 9-521-55432-2
- G. HART
Archimedean Duals
Virtual polyhedra - The Encyclopedia of Polyhedra
- INTERNATIONAL UNION of CRYSTALLOGRAPHY
International Tables for Crystallography, Vol. A
Theo Hahn Editor, Kluwer Academic Publisher, 1989


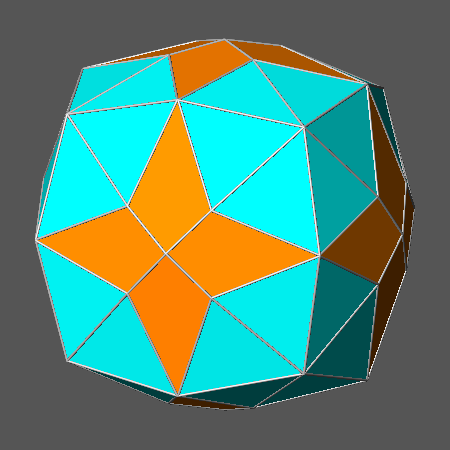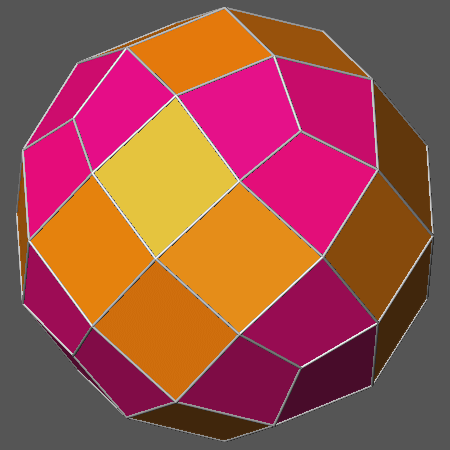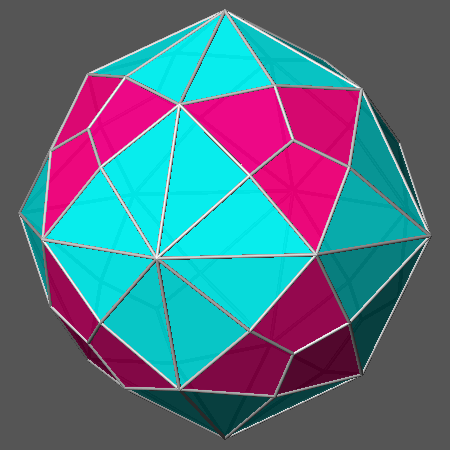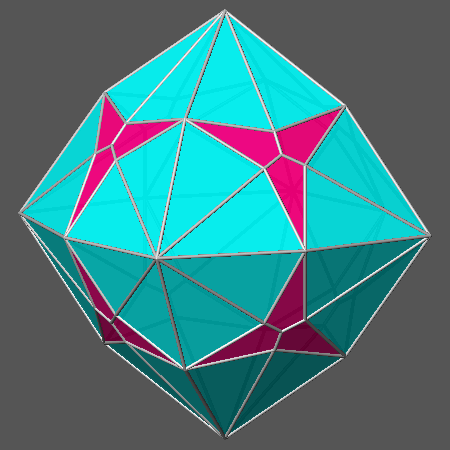



_intersection_(RD_&CO_).png)

_scaled7.png)
_intersection_(CO&RD)&dual_211.png)
&211).gif)
&211).png)

_new.gif)
.png)






_.png)
_new.gif)
_compound_.png)


.png)

.gif)
&dual).png)
_new.png)
_new.gif)
_compound.png)




.gif)

_scaled04.png)
_new.gif)
_04.png)






_scaled.png)
_new.gif)
_scaled.png)
&dual_(RCO&dual)_scaled.png)
&(dual_(RCO&dual))_.gif)
&(dual_(RCO&dual))_.png)









&dual211).gif)
&dual)).gif)