 |
 |
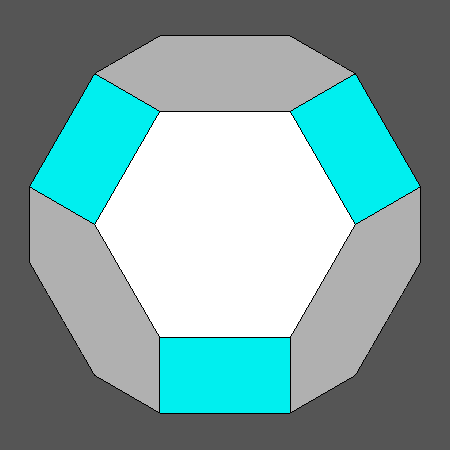
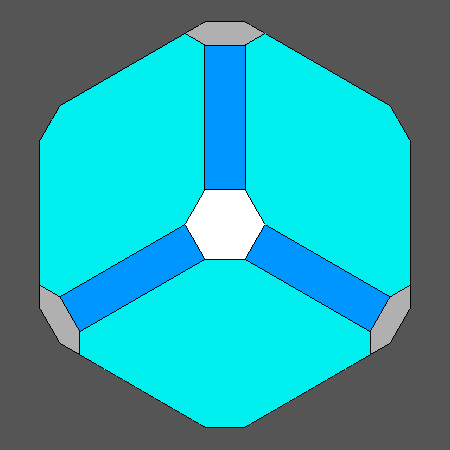
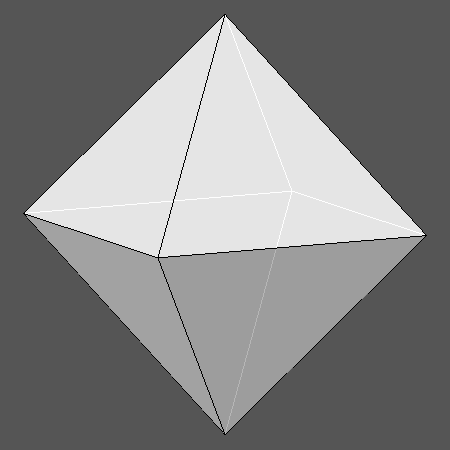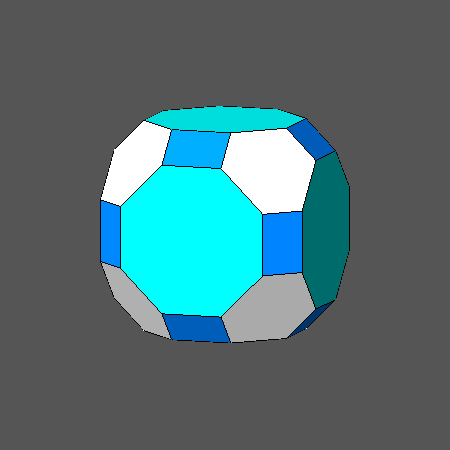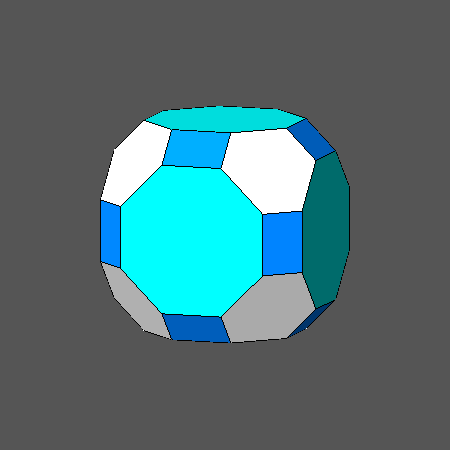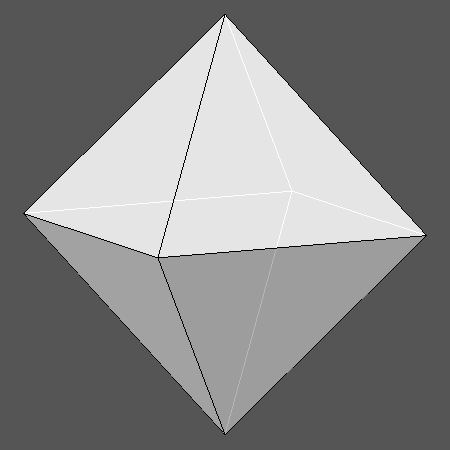
| Fig.1a) View, normal to its (111) regular hexagonal face, of the Archimedean truncated octahedron (AtO) | Fig.1b) View, normal to its (100) regular octagonal face, of the Archimedean truncated cube (AtC) |
Livio Zefiro*
*Dip.Te.Ris, Universita' di Genova, Italy
(E-mail address:
livio.zefiro@fastwebnet.it)
Notes
|
 |
 |
| Fig.1a) View, normal to its (111) regular hexagonal face, of the Archimedean truncated octahedron (AtO) | Fig.1b) View, normal to its (100) regular octagonal face, of the Archimedean truncated cube (AtC) |
|
Truncation by a rhomb-dodecahedron (RD) of the cuboctahedron (CO) and the Archimedean truncated octahedron (AtO) and truncated cube (AtC) |
|||
| CO | AtO | AtC | |
| dcube /doctahedron | √3/2 | 2/√3 | √6-√3 |
| Indices of the Catalan dual | {110} | {210} | {11 √2-1} |
|
If dRD =1,
the rhomb-dodecahedron is tangent to CO, AtO and AtC, respectively, in coincidence with the following values: |
|||
| dcube | √2/2 | 2√2/3 | √2/2 |
| doctahedron | √2/√3 | √2/√3 | (√2+1)/√6 |
|
Vertex-transitive solids |
|||
| dRD | (2+√2)/4 = 0.8535 | (4+√2)/6 = 0.9024 | |
| Indices of the dual hexakis-octahedra | {√2 1 √2-1} | {2√2 1 √2-1} | |
| In each dual the eight dihedral angles
between contiguous faces sharing a vertex along [100] are equal and measure: |
26.899° | 15.722° | |
|
Vertex-transitive solids |
|||
| dRD | 5/6 = 0.8333 | (4+√2)/6 = 0.9024 | |
| Indices of the dual hexakis-octahedra | {321} | {3 √2+1 2√2-1} | |
|
In each dual the six dihedral angles between contiguous faces sharing a vertex along [111] are equal and measure: |
21.787° | 11.152° | |
|
Vertex-transitive solids with square |
|||
| dRD | 3/4 | 5/6 = 0.8333 | (2+√2)/4 = 0.8535 |
| Indices of the dual deltoid-icositetrahedra | {211} | {411} | {√2 11} |
|
In each dual, the three dihedral angles
between contiguous faces sharing a vertex along [111] are equal and measure: |
33.557° | 60° | 16.842° |
|
In each dual, the four dihedral angles between contiguous faces sharing a vertex along [100] are equal and measure: |
48.190° | 27.266° | 60° |
| Zone axis of the dual forms | |||
| [uvw] such as hu+kv+lw=0 | [1 1 1] | [1 2 2] | [√2 1 1] |
|
Archimedean truncated cuboctahedron (tCO), rhomb-cuboctahedron (RCO) and solids including regular faces, obtained by varying the central distance of the intersecting rhomb-dodecahedron |
||
| RCO | tCO | |
| dcube /doctahedron | √3/(2√2-1) | (3-√2)/√3 |
| dRD /doctahedron | √3/(2√2-1) | (2√2-1)/√3 |
| If dRD =1: | ||
| dcube | 1 | (5√2-1)/7 |
| doctahedron | (2√2-1)/√3 | √3/(2√2-1) |
| Indices of the Catalan duals | {√2+1 1 1} |
{3-√2 1 √2-1} |
| In each Catalan solid, the dihedral angles between each couple of contiguous faces are equal and measure: | 41.882° | 24.918° |
|
Solids including regular octagonal faces of cube |
||
| dRD | (3√2-2)/2 | 1 |
| Indices of the dual hexakis-octahedra | {√2+1 √2 2-√2} | {3-√2 1 √2-1} |
In each dual, the eight dihedral angles between contiguous faces sharing a vertex along [100] are equal and measure:
|
23.650° | 24.918° |
|
Solids including regular hexagonal faces of octahedron |
||
| dRD | (√2+2)/3 |
1 |
| Indices of the dual hexakis-octahedra | {3(√2+1) 3+√2 3-√2} |
{3-√2 1 √2-1} |
|
In each dual, the six dihedral angles between contiguous faces sharing a vertex along [111] are equal and measure:
|
26.804° | 24.918° |
|
Solids including both square faces of cube and equilateral triangular faces of octahedron |
||
| dRD | 1 | (11+√2)/14 |
| Indices of the dual deltoid-icositetrahedra | {√2+1 1 1} | {3√2-2 1 1} |
|
In each dual, the three dihedral angles between contiguous faces sharing a vertex along [111] are equal and measure:
|
41.882° | 38.709° |
|
In each dual, the four dihedral angles between contiguous faces sharing a vertex along [100] are equal and measure:
|
41.882° | 44.317° |
|
Non-Archimedean truncated octahedra deriving from RCO and tCO by increasing the value of dRD |
||
| dRD | (4-√2)/2 | 3/(4-√2) |
| Indices of the dual tetrakis-hexahedra | {√2+1 2 0} | {3-√2 √2 0} |
|
In each dual, the four dihedral angles between contiguous faces sharing a vertex along [100] are equal and measure:
|
53.629° | 56.151° |
| Zone axis of the dual forms | ||
| [uvw] such as hu+kv+lw=0 | [2(√2-1) 1 1] | [√2 √2-3 √2-3] |
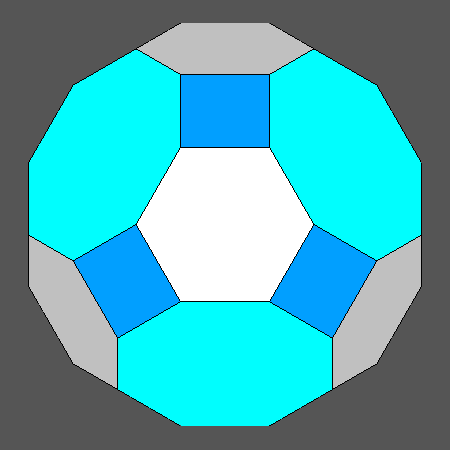
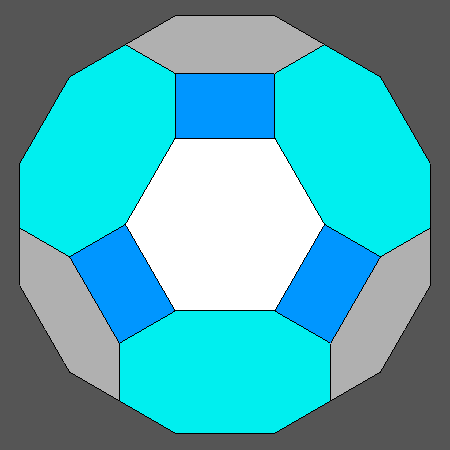
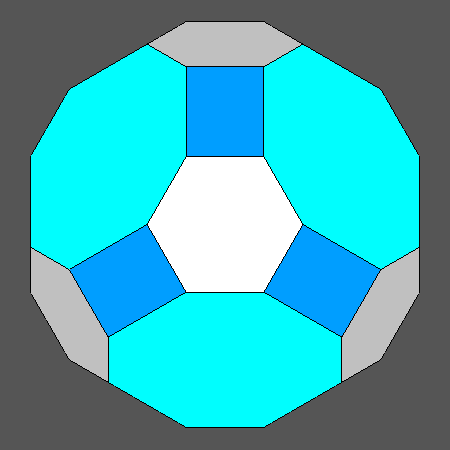
Fig.2 shows the views, along the [111] direction, of the solids including regular hexagonal faces (as the Archimedean truncated octahedron already shown in Fig.1, on the left), which can be obtained by the intersection of cube, octahedron and rhomb-dodecahedron.
|
View along the [111] direction of cubic forms including regular hexagonal faces derived from the intersection of Archimedean polyhedra with a rhomb-dodecahedron, compared with the Archimedean truncated cuboctahedron |
|
 |
 |
|
Archimedean truncated cuboctahedron (tCO) |
Polyhedron with regular hexagonal faces derived from the rhomb-cuboctahedron (RCO) by varying the central distance of the rhomb-dodecahedron but letting unchanged the ratio dcube/doctahedron |
 |
 |
|
Polyhedron including regular hexagonal faces derived from the truncation of the Archimedean cuboctahedron (CO) by a rhomb-dodecahedron |
Polyhedron including regular hexagonal faces derived from the truncation of the Archimedean truncated cube (AtC) by a rhomb-dodecahedron |
|
View along the [100] direction of cubic forms, derived from the intersection of Archimedean solids with a rhomb-dodecahedron and including regular octagonal faces of cube, compared with the Archimedean truncated cuboctahedron |
|
 |
 |
|
Archimedean truncated cuboctahedron (tCO) |
Polyhedron including regular octagonal faces derived from the rhomb-cuboctahedron (RCO) by varying the central distance of the rhomb-dodecahedron but letting unchanged the ratio dcube/doctahedron |
 |
 |
|
Polyhedron including regular octagonal faces, derived from the truncation of the cuboctahedron (CO) by a rhomb-dodecahedron |
Polyhedron including regular octagonal faces, derived from the truncation of the Archimedean truncated octahedron (AtO) by a rhomb-dodecahedron |
|
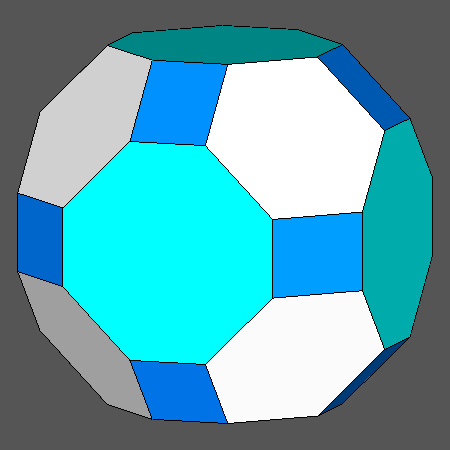
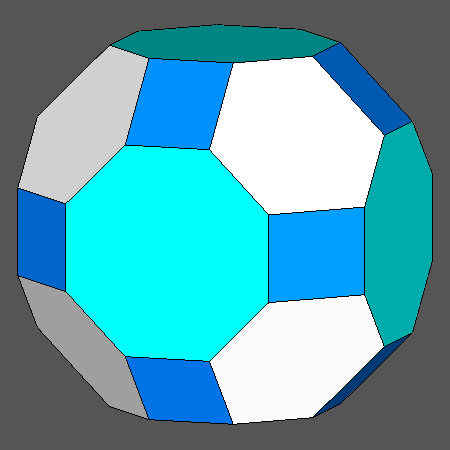
Truncated cuboctahedron (tCO) compared with the four similar polyhedra, including regular hexagonal or octagonal faces, obtained by intersecting the rhomb-cuboctahedron (RCO) and the cuboctahedron (CO) with a rhomb-dodecahedron |
|
 |
 |
|
Polyhedron derived from RCO, including regular hexagonal faces
of octahedron |
Polyhedron derived from RCO, including regular octagonal faces
of cube
|
|
|
|
|
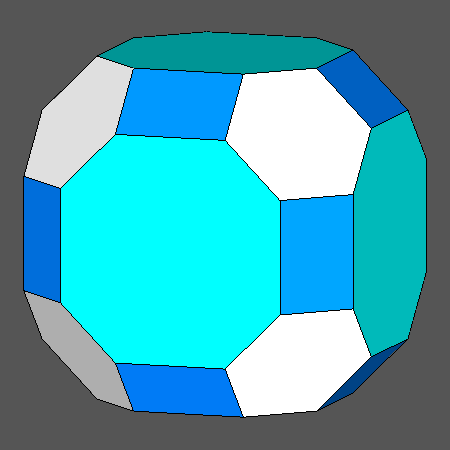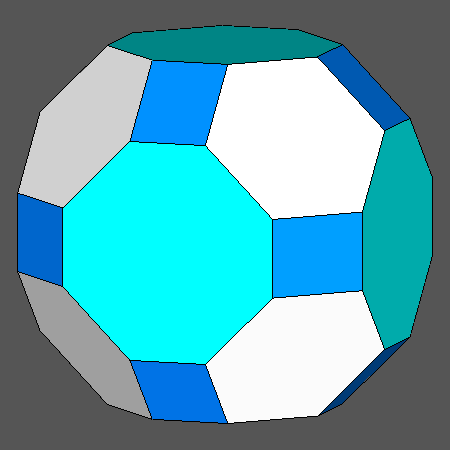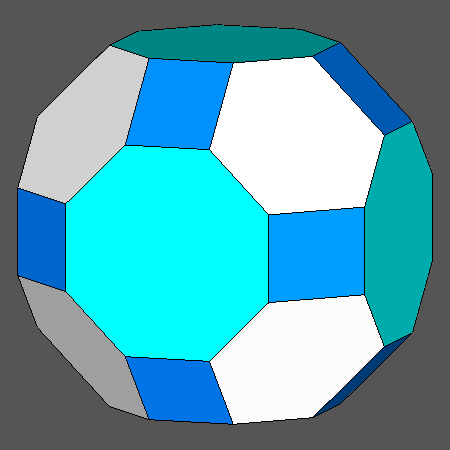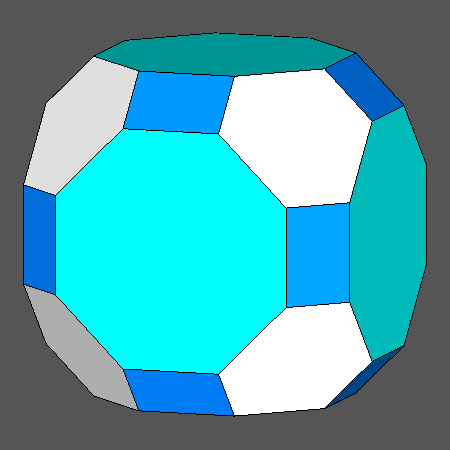
Being an Archimedean solid, the truncated cuboctahedron (tCO) includes only regular faces: six octagonal faces of cube, eight hexagonal faces of octahedron and twelve square faces of rhomb-dodecahedron |
|
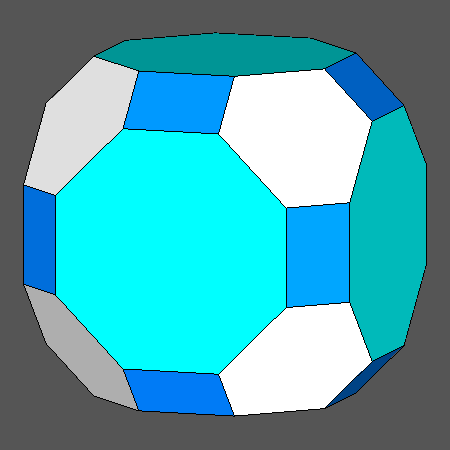 |
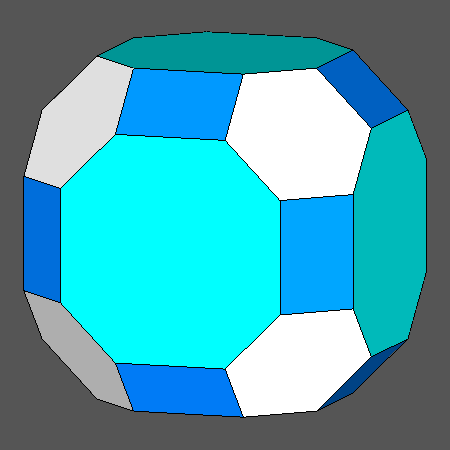 |
|
Polyhedron derived from CO, including regular octagonal faces
of cube
|
Polyhedron derived from CO, including regular hexagonal faces
of octahedron |
|
Comparison between the Catalan hexakis-octahedron, dual of the Archimedean truncated cuboctahedron (tCO), and four very similar hexakis-octahedra, dual of polyhedra derived from CO and RCO which include faces having an octagonal or hexagonal regular shape |
|
 |
 |
|
Hexakis-octahedron
{3(√2+1) 3+√2 3-√2}
dual of the solid, derived from RCO, including regular hexagonal faces. |
Hexakis-octahedron
{√2+1 √2 2-√2}
dual of the solid, derived from RCO, including regular octagonal faces. |
|
|
|
|
Hexakis-octahedron {3-√2 1 √2-1}, dual of the Archimedean truncated cuboctahedron (tCO): as it is a Catalan solid, all the dihedral angles between each couple of edge-sharing faces are equal and measure = 24.918° |
|
 |
 |
|
Hexakis-octahedron
{√2
1 √2-1} dual of the solid, derived from CO,
including regular octagonal faces.
|
Hexakis-octahedron {321} dual of the solid, derived from CO, including regular hexagonal faces.
|
 |
 |
|
Animated sequence highlighting the differences between the truncated cuboctahedron and the solids, including hexagonal or octagonal regular faces, derived from the cuboctahedron (CO) and the rhomb-cuboctahedron (RCO). |
Animated sequence highlighting the small differences between the Catalan hexakis-octahedron, dual of tCO, and the other hexakis-octahedra, which are the duals of solids, including hexagonal or octagonal regular faces, derived from CO and RCO. |
|
Comparison between the intersection of tCO with the dual Catalan hexakis-octahedron and the intersection with the relative duals of the polyhedra, derived from the Archimedean CO and RCO, which include hexagonal or octagonal regular faces |
|
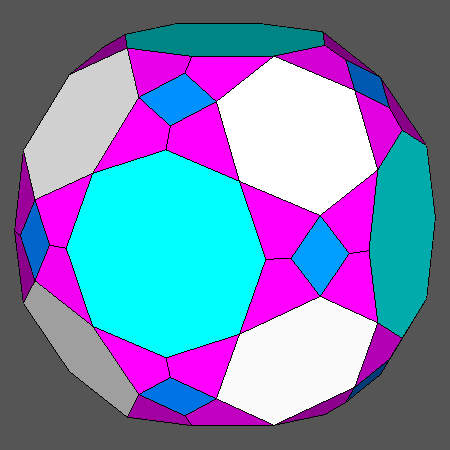 |
 |
|
Solid resulting from the intersection with its dual of the polyhedron, derived from RCO, including regular hexagonal faces of octahedron. |
Solid resulting from the intersection with its dual of the polyhedron, derived from RCO, including regular octagonal faces of cube. |
|
|
|
|
Solid resulting from the intersection between the Archimedean truncated cuboctahedron (tCO) and the dual Catalan hexakis-octahedron, including square, regular hexagonal and regular octagonal faces. |
|
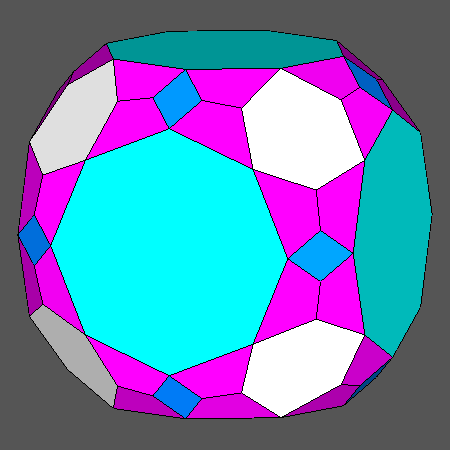 |
 |
|
Solid resulting from the intersection with its dual of the polyhedron, derived from CO, including regular octagonal faces of cube. |
Solid resulting from the intersection with its dual of the polyhedron, derived from CO, including regular hexagonal faces of octahedron. |
|
Duals of the polyhedra obtained from the intersection between solids including regular faces derived from Archimedean polyhedra and the relative duals |
|
.png) |
_.png) |
|
Solid derived from RCO, in which all the six dihedral angles between each couple of contiguous faces sharing a vertex along [111] measure 23.817° |
Solid derived from RCO, in which all the eight dihedral angles between each couple of contiguous faces sharing a vertex along [100] measure 22.306° |
|
|
|
|
Solid dual of the intersection between the Archimedean
truncated octahedron and the dual Catalan hexakis-octahedron, made of the
deltoid-icositetrahedron
{3√2-2
1 1},
the triakis-octahedron
{3+√2 3+√2
√2}
and the
tetrakis-cube
{3-√2
1 0} In it: |
|
 |
.png) |
|
Solid derived from CO, in which all the eight
dihedral angles between each couple of contiguous faces sharing a vertex along [100] measure 25.529° |
Solid derived from CO, in which all the six dihedral angles between each couple of contiguous faces sharing a
vertex along [111] measure 19.188° |
 |
.gif) |
|
Animated sequences highlighting the differences which characterize the solids reported in Fig.7 and Fig.8 |
|
|
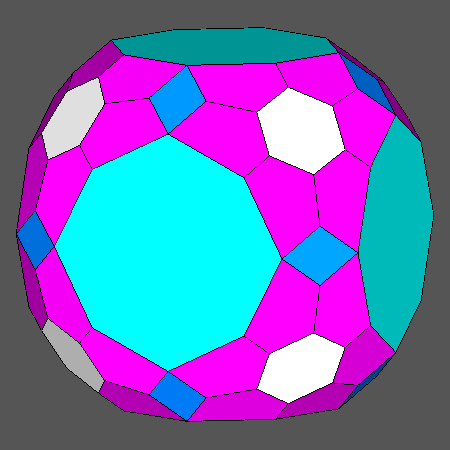
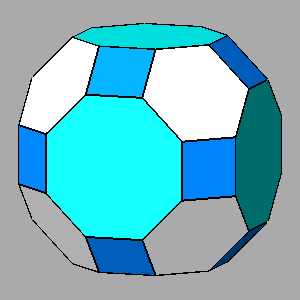
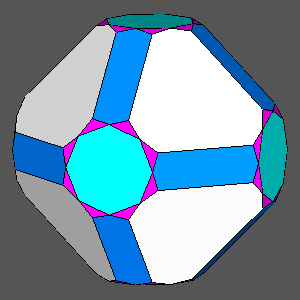
Comparison between the truncated cuboctahedron and the polyhedra, including regular faces, derived from the intersection with a rhomb-dodecahedron (RD) of the Archimedean truncated cube (AtC) and truncated octahedron (AtO); in addition, their duals and other related composite forms are shown. |
||
 |
 |
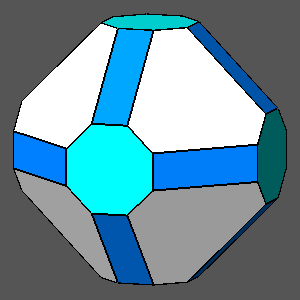 |
| Polyhedron with regular hexagonal faces derived from the truncation by RD of the Archimedean truncated cube (AtC) | Archimedean truncated cuboctahedron | Polyhedron with regular octagonal faces derived from the truncation by RD of the Archimedean truncated octahedron (AtO) |
 |
 |
 |
|
Hexakis-octahedron
{3√2+1 2√2-1}
dual of the solid with regular hexagonal faces derived from the Archimedean truncated cube (AtC) |
Hexakis-octahedron {3-√2
1
√2-1} It is the Catalan dual of the Archimedean truncated cuboctahedron
|
Hexakis-octahedron
{2√2
1 √2-1} dual of the solid with regular octagonal faces derived from
the Archimedean truncated octahedron (AtO) |
 |
 |
 |
|
Solid including regular hexagonal faces,
obtained from the intersection of the polyhedron derived from AtC with its dual |
Solid resulting from the intersection with its Catalan dual of the Archimedean truncated cuboctahedron |
Solid including regular octagonal faces,
obtained from the intersection of the polyhedron derived from AtO with its dual |
_.png) |
.png) |
.png) |
|
Solid derived from AtC, in which all the dihedral angles between the six couples of contiguous faces sharing a vertex along [111]
measure 9.70° |
Solid dual of the intersection between the Archimedean truncated cuboctahedron and the dual Catalan hexakis-octahedron
(the values of the dihedral angles have already been reported in Fig.8) |
Solid derived from AtO, in which all the dihedral
angles between the eight couples of contiguous faces sharing a vertex along [100] measure 14.657° |
The sequences of solids including regular-shaped faces, obtained by the intersection with RD of non Archimedean truncated octahedra or truncated cubes belonging to the different intervals just defined, are visualized in Fig.11.
|
Solids which include faces having the shape of regular polygons, obtained by the intersection with the rhomb-dodecahedron of generic non-Archimedean truncated octahedra and truncated cubes, compared with the Archimedean truncated cuboctahedron |
||
| Truncated octahedra and truncated cubes |
Vertex-transitive solids which include regular faces having hexagonal, octagonal or square shape |
Vertex-transitive solids including square faces together with triangular equilateral faces |
|
2√3/3 < dcube /doctahedron
< √3
|
||
_1.1785_d(O)_0.8165_d(R)_1.0_.png) |
_1.1785_d(O)_0.8165_d(R)_0.95118_.png) |
_1.1785_d(O)_0.8165_d(R)_0.91666_.png) |
|
dRD = 1 |
dRD = 0.951: octagonal regular faces | dRD = 0.917 |
|
√3/(2√2-1) < dcube
/doctahedron
<
2√3/3 |
||
_0.8485_d(O)_0.8165_d(R)_1.0_.png) |
_0.8485__d(O)_0.8165_two_frames.gif) |
_0.8485_d(O)_0.8165_d(R)_0.8_dual_trap_.png) |
|
dRD = 1 |
dRD
= 0.933: hexagonal regular faces dRD = 0.883: octagonal regular faces |
dRD = 0.8 |
|
(3-√2)√3/3
< dcube /doctahedron
< √3/(2√2-1) |
||
_0.7605_d(O)_0.8165_.png) |
_0.7605__d(O)_0.8165_three_frames.gif) |
_0.7605_d(O)_0.8165_d(R)_0.76888_dual_trap.png) |
|
dRD = 1 |
dRD = 0.871 : hexagonal regular faces dRD = 0.865 : octagonal regular faces dRD = 0.818 : square faces |
dRD = 0.769 |
|
dcube /doctahedron = (3-√2)/√3 |
||
_0.74755_d(O)_0.8165_from_tCO.png) |
_0.74755_d(O)_0.8165_d(R)_86193_tCO_.png) |
_0.74755_d(O)_0.8165_d(R)_0.7643_dual_trap_from_tCO.png) |
dRD = 3/(4-√2)
=1.160 implies tangency of the rhomb-dodecahedron {110} to the truncated octahedron in which:
doct = √3/(2√2-1), dcube = (5√2-1)/7 |
An Archimedean solid, the truncated cuboctahedron (tCO), results if also:
doctahedron /dRD
= √3/(2√2-1)
It follows that, when dRD = 1:
doct =
√3/(2√2-1),
dcube = (5√2-1)/7
|
When dRD
= (√2+11)/14 = 0.887,
each vertex is shared by four faces if:
doct =
√3/(2√2-1),
dcube = (5√2-1)/7
|
|
Alternatively,
dRD = 1 implies tangency to the truncated octahedron in which: doctahedron= √2/√3 and dcube= √2(3-√2)/3 |
The Archimedean tCO can be obtained when dRD =
(4-√2)/3
= 0.862 if:
doctahedron= √2/√3 and dcube= √2(3-√2)/3 |
When dRD=
(6-√2)/6= 0.764, each vertex is shared by four faces if:
doctahedron=
√2/√3
and dcube=
√2(3-√2)/3
|
|
√3/2 < dcube
/doctahedron
< (3-√2)/√3
|
||
_0.7273_d(O)_0.8165_.png) |
_0.7273__d(O)_0.8165_.gif) |
_0.7273_d(O)_0.8165_d(R)_0.75715_dual_trap_.png) |
|
dRD = 1 |
dRD
= 0.931 : square faces dRD = 0.858 : octagonal regular faces dRD = 0.848 : hexagonal regular faces |
dRD = 0.757 |
|
√3/(√2+1)
< dcube /doctahedron
< √3/2
|
||
_0.7071_d(O)_0.8931_.png) |
_0.7071__d(O)_0.8931.gif) |
_0.7071_d(O)_0.8931_d(R)_0.79692_dual_trap_.png) |
|
dRD = 1 |
dRD
= 0.920 : octagonal regular faces dRD = 0.865 : hexagonal regular faces |
dRD = 0.797 |
|
√3/3 < dcube /doctahedron
< √3/(√2+1) |
||
_0.7071_d(O)_1.0922_.png) |
_0.7071_d(O)_1.0922_d(R)_0.94590_hexag.png) |
_0.7071_d(O)_1.0922__d(R)_0.91885_dual_trap.png) |
|
dRD = 1 |
dRD = 0.946 : hexagonal regular faces |
dRD = 0.919 |
|
Relations holding between the central distance of the truncating rhomb-dodecahedron and the central distances of cube and octahedron in case of each series of solids including regular faces |
|
Vertex-transitive solids including regular hexagonal faces of octahedron |
| dRD = (doctahedron +√3 dcube )/√6 when the ratio dcube/doctahedron varies in the range √3/3 < dcube /doctahedron ≤ 2√3/3 |
|
Vertex-transitive solids including regular octagonal faces of cube |
| dRD = (√3 doctahedron + (√2-1) dcube)/2 when the ratio dcube/doctahedron varies in the range (√2-1)√3 ≤ dcube /doctahedron<√3 |
|
Vertex-transitive solids including square faces of rhomb-dodecahedron |
| dRD = (√2+1) (√3doctahedron -√2 dcube) when the ratio dcube/doctahedron varies in the range √3/2 < dcube /doctahedron <√3/(2√2-1) |
|
Vertex-transitive solids including square faces of cube and triangular equilateral faces of octahedron |
| dRD = √2 (√3doctahedron + dcube )/4 when the ratio dcube/doctahedron varies in the range √3/3 < dcube /doctahedron <√3 |
|
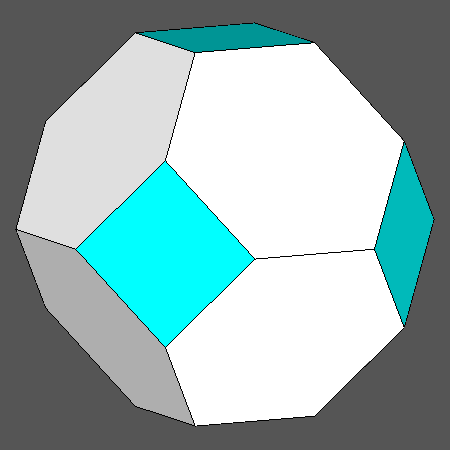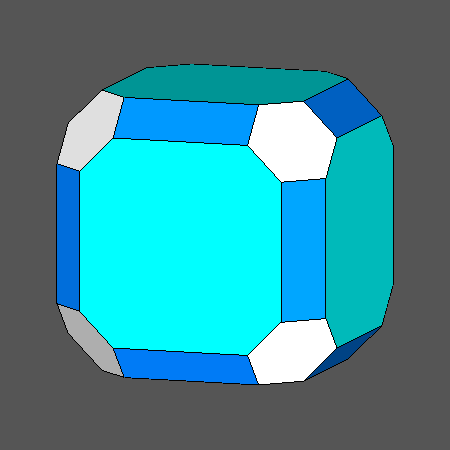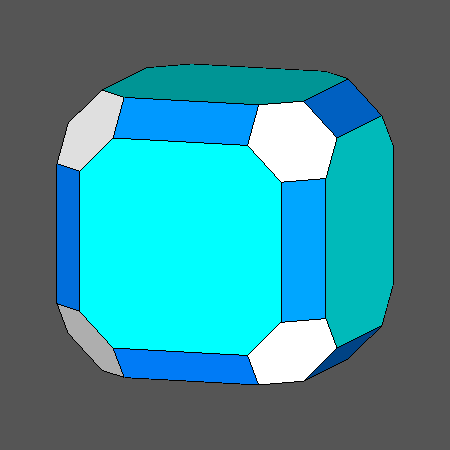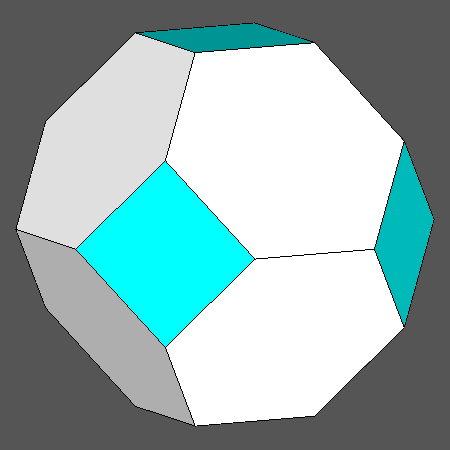
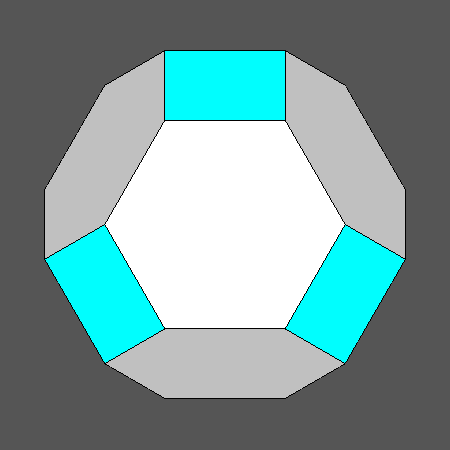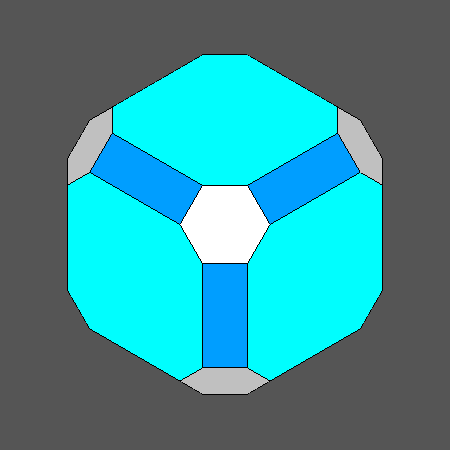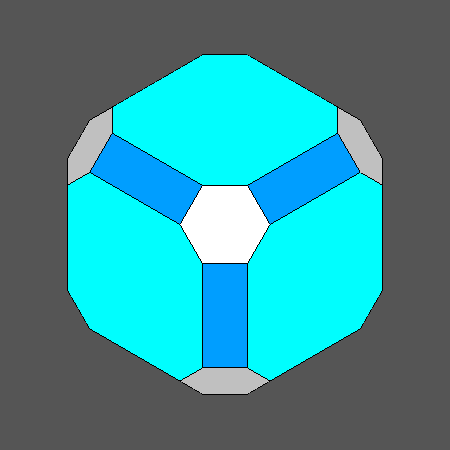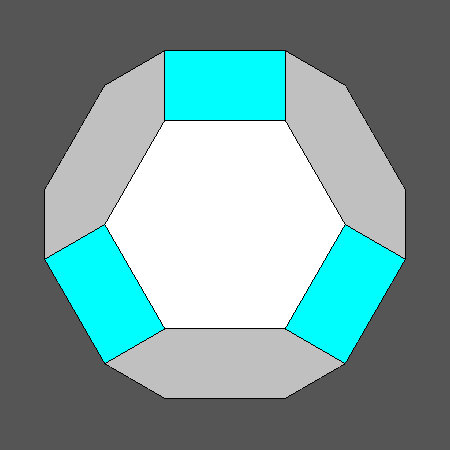
Set of vertex-transitive solids including regular hexagonal faces of octahedron |
|
 |
 |
|
Orthographic view of the sequence of solids, going from the Archimedean truncated octahedron to the cube and including also the Archimedean truncated cuboctahedron, characterized by regular hexagonal faces of octahedron |
View along the [111] 3-fold axis, normal to an hexagonal face of octahedron, of the sequence on the left |
|
Set of vertex-transitive solids including regular octagonal faces of cube |
|
 |
 |
|
Orthographic view of the sequence of solids, going from the octahedron to the Archimedean truncated cube and including also the Archimederan truncated cuboctahedron, characterized by regular octagonal faces of cube |
View along the [100] 4-fold axis, normal to an octagonal face of cube, of the sequence on the left |
|
Set of vertex-transitive solids including square faces of rhomb-dodecahedron |
|
 |
 |
|
Orthographic view of the sequence of solids, going from the cuboctahedron to the rhomb-cuboctahedron and including also the truncated cuboctahedron, characterized by square faces of rhomb-dodecahedron |
View along the [110] 2-fold axis, normal to a square face of rhomb-dodecahedron, of the sequence on the left |
|
Set of vertex-transitive solids including square faces of cube and equilateral triangular faces of octahedron |
|
 |
 |
|
Orthographic view of the sequence of solids, going from the cube to the octahedron and including also the Archimedean rhomb-cuboctahedron, characterized by square faces of cube and equilateral triangular face of octahedron. |
View of the same sequence along the [100] 4-fold axis, normal to a square face of each solid of the series. |
 |
 |
|
View of the same sequence along the [110] 2-fold axis, normal to
an usually rectangular face of each solid of the series. |
View of the same sequence along the [111] 3-fold axis, normal to an equilateral triangular face of
each solid of the series. |
|
Solids which include faces having the shape of regular polygons, obtained from the intersection of each truncated tetrahedron with a cube |
||
 |
 |
 |
|
Pseudo octahedron resulting from the
intersection of two tetrahedra having an equal central distance:
d{111} =
d{111}
= √3/3 |
Pseudo Archimedean truncated octahedron
resulting from the intersection of the pseudo octahedron (on the left) with a cube when:
dcube = 2/3
|
Pseudo Archimedean cuboctahedron resulting from the intersection of the pseudo octahedron with a cube when:
dcube
= 1/2 |
 |
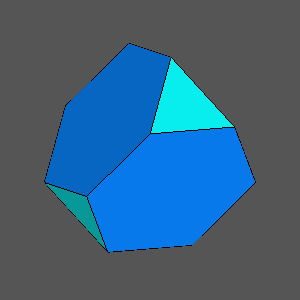
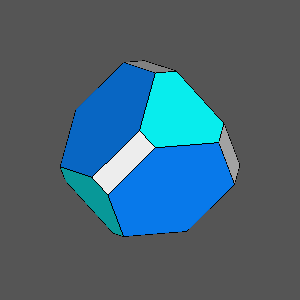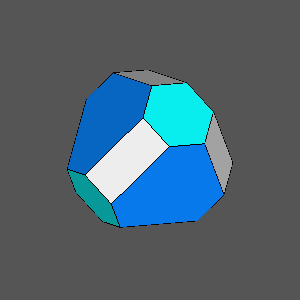 |
 |
|
Truncated tetrahedron |
Solids with {111} or {111} faces having the shape
of regular hexagons, as result of the intersection of the truncated tetrahedron (on the left) with a cube,
whose faces are set sequentially at the following distances from the barycenter:
dcube = 5/6 and
dcube = 13/18 |
Solid (dual of a deltoid-dodecahedron), including {111} and {111} equilateral triangular faces,
obtained when the central distance of the cube intersecting the truncated tetrahedron is:
dcube = 7/12
|
 |
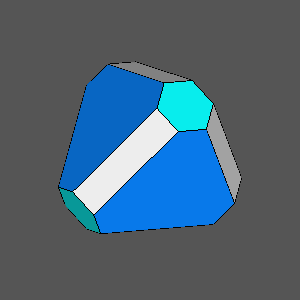 |
 |
|
Archimedean truncated tetrahedron, including regular hexagonal faces of the tetrahedron
{111}
d{111} = 5√3/9;
d{111}
= √3/3 |
Solid with regular hexagonal faces of the {111} tetrahedron, derived from the intersection of the Archimedean truncated tetrahedron
with a cube when:
dcube = 7/9 |
Solid (dual of a deltoid-dodecahedron), including {111} and {111} equilateral triangular faces,
obtained when the central distance of the cube which intersects the Archimedean truncated tetrahedron is:
dcube = 2/3
|
 |
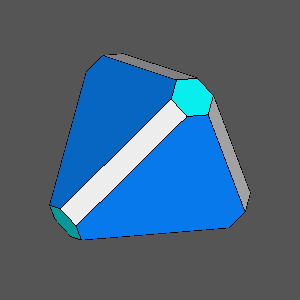 |
 |
|
Truncated tetrahedron |
Solid with regular hexagonal faces of the {111} tetrahedron,
resulting from the intersection of the truncated tetrahedron shown on the left with a cube when:
dcube = 5/6 |
Solid (dual of a deltoid-dodecahedron), including {111} and {111} equilateral triangular faces,
obtained when the central distance of the cube which intersects the truncated tetrahedron is:
dcube = 3/4
|
|
Duals of solids, including regular faces, obtained by intersecting an Archimedean truncated tetrahedron and a pseudo octahedron with a cube |
||
 |
 |
 |
|
Triakis-tetrahedron {311}: it is the dual of the Archimedean truncated tetrahedron in which the faces of the tetrahedron
{111} are nearer to the center of the solid
(d{111} /d{111}=
5/3) |
Cube: it is the dual of the pseudo-octahedron obtained from the intersection of the couple of tetrahedra {111}
and {111} when:
d{111} /d{111}=
1
|
Triakis-tetrahedron {311}:
it is the dual of the Archimedean truncated tetrahedron in which the faces of the tetrahedron
{111} are nearer to the center of the solid
(d{111} /d{111}=
3/5) |
 |
 |
 |
|
Hexakis-tetrahedron {753}: dual of the solid, including regular hexagonal faces, derived from the intersection of the Archimedean truncated tetrahedron (in which d{111}/d{111}= 5/3) with a cube, when dcube = 7/9 |
Tetrakis-hexahedron {210}: dual of the pseudo Archimedean truncated octahedron resulting from the intersection of a pseudo-octahedron (obtained from two tetrahedra if: d{111}/d{111}= 1) with a cube, when dcube = 2/3 |
Hexakis-tetrahedron {753}: dual of the solid including regular hexagonal faces derived from the intersection of the Archimedean truncated tetrahedron (in which d{111}/d{111}= 3/5) with a cube, when dcube = 7/9 |
 |
 |
 |
|
Deltoid-dodecahedron {221}: dual of the solid, including equilateral triangular and square faces,
derived from the intersection with a cube (when dcube = 2/3) of
the Archimedean truncated tetrahedron (in which:
d{111} /d{111}= 5/3)
. |
Rhomb-dodecahedron {110}: dual of the pseudo cuboctahedron resulting from the intersection of a pseudo-octahedron (obtained if:
d{111}/d{111}= 1)
with a cube, when dcube = 1/2.
|
Deltoid-dodecahedron {221}: dual of
the solid including regular triangular
and square faces, derived from the intersection with a cube (when dcube = 2/3) of the Archimedean truncated tetrahedron (in which:
d{111} /d{111}= 3/5).
|
|
Relations holding between the central distance of the truncating cube and the central distances of the two tetrahedra in case of each series of solids including regular faces |
|
Vertex-transitive solids including regular hexagonal faces of the tetrahedron {111} |
| dcube = √3(d{111}+ 3d{111})/6 when the ratio d{111}/d{111} varies in the range 3/5 ≤ d{111}/d{111} < 3 |
|
Vertex-transitive solids including regular hexagonal faces of the tetrahedron {111} |
| dcube = √3(d{111}+ 3d{111})/6 when the ratio d{111}/d{111} varies in the range 1/3 ≤ d{111}/d{111} < 5/3 |
|
Vertex-transitive solids including triangular equilateral faces of both tetrahedra |
| dcube = √3(d{111}+ d{111})/4 when the ratio d{111}/d{111} varies in the range 1/3 < d{111}/d{111} < 3 |
 |
 |
 |
 |
|
Animated sequence relative to the solids characterized by regular hexagonal faces of the tetrahedron {111} (on the left) or {111} (on the right), deriving from the intersection with a cube of two series of truncated tetrahedra (obtained as the ratio d{111}/d{111} varies within proper ranges). In each sequence, the only frame in which the faces of both tetrahedra have a regular hexagonal shape concerns the pseudo Archimedean truncated octahedron, obtained when the central distances of the two tetrahedra are equal and dtetrahedra /dcube = √3/2. |
|