4. COGNITIVE VISUALIZATION
OF CONTINUUM PROBLEM
"Transfinite Numbers themselves are, in a certain sense, new irrationalities. Indeed, in my opinion, the method for the definition of finite irrational numbers is quite analogous, I can say, is the same one as my method for introducing transfinite numbers. It can be certainly said: transfinite numbers stand and fall together with finite irrational numbers."
- Georg Cantor.
Denote the tree in Fig. 1 by TR,
rotate the tree TR counter-clockwise at 90°
and place a mirror AB at its root V in parallel to its levels. The visual result
of such transformation we can see in Fig. 2, that
demonstrates a Cognitive-Visual image of the mirror-like
1-1-correspodence, say Y,
between the initial tree TR
and its mirror image - the tree TL.
The interpretation of the levels of the trees TR
and TL is also given in Fig. 2.
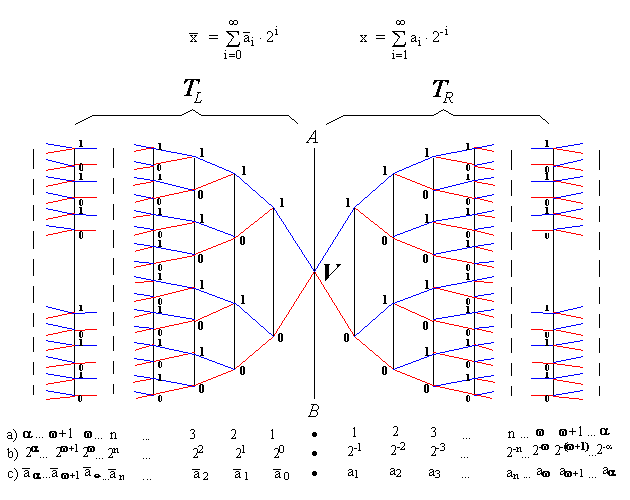
Fig. 2. Cognitive Visualization of Continuum Problem and the hyper-real numbers system:
a) level numbers of the trees;
b) powers of the base 2 in the binary system;
c) binary representation of the "in-both-side transfinite" hyper-real numbers.
|