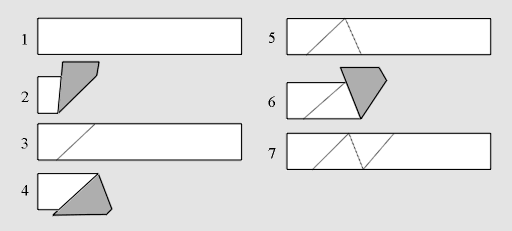
|
Figure 1: 1) Begin with a long strip of gummed tape; 2) Fold UP - any way will do;
3) Unfold; 4) Fold DOWN - now you must do it exactly as shown; 5) Unfold;
6) Fold UP, exactly as shown; 7) Unfold.
|
Now go to frame 4, and keep repeating the folding in frames 4 through 7, to
make a string of triangles as long as you need. Notice two things. First,
the folding procedure, after your initial fold, goes DOWN, UP, DOWN, UP,...
We will abbreviate this folding procedure by D1U1
and call the tape produced the D1U1-tape.
2 Second, you can readily see that, as
we claimed, the triangles become
more and more regular as you fold. Thus, if you wish to use this tape to
construct models requiring equilateral triangles, all that you need to do is
compare successive triangles, beginning with the first one formed, until it
is not possible to detect any difference between them - and then throw away
the defective ones and continue to fold, in the prescribed manner, to obtain
the equilateral triangles you need for the
constructions in Section 3. (We
show in [Math] how to prove
that all angles on this tape do, in
fact, approach p/3.)
To fold tape from which you can construct regular pentagons simply follow the
instructions in the numbered frames of Figure 2.
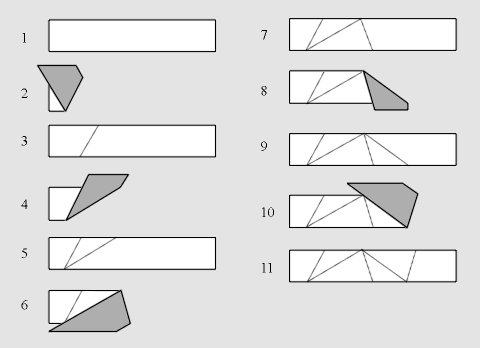
|
Figure 2: 1) Begin with a long strip of gummed tape; 2) Fold UP - any way will do;
3) Unfold; 4) Fold DOWN - now you must do it exactly as shown; 5) Unfold;
6) Fold UP, exactly as shown; 7) Unfold; 8) Fold DOWN, exactly as shown; 9) Unfold;
10) Fold UP, exactly as shown; 11) Unfold.
|
Now go to frame 4, and keep repeating the folding in frames 4 through 11, to
make a string of tape from which you will be able to construct regular
pentagons. First, notice that the folding process, after the first two
initial folds, goes DOWN, DOWN, UP, UP, DOWN, DOWN, UP, UP,... We will
abbreviate this folding procedure by D2U2
and call the tape produced
the D2U2-tape.
Second, notice that this tape has two kinds of crease
lines, which we will refer to as short and long crease lines. Third, it is
evident that the configuration formed by these crease lines is becoming more
and more regular, reproducing the same angles at each edge of the tape. (We
show in [Math] how to prove that the smallest angles on this
tape do, in fact, approach p/5.)
This is the tape that you will use to make regular pentagons and models with
regular pentagonal faces. To see how this works throw away the first few
triangles you have folded (10 will be very safe) and continue to fold, in the
prescribed manner, to obtain the tape you need to produce the constructions
in Section 3. Just to practise now, cut
off a piece of tape and make the
pentagon shown in Figure 3. Notice that when you constructed this pentagon
you cut the D2U2-tape
along a short crease line, and folded on short
crease lines.