|
D
A ×E |
= |
(-1)r+k(-s+k+l-1)!
(r+k)!(-n+l-1)! |
. |
(-1)s-l(s-l)!(-n+l+1)!
(-r-1)! |
. |
(r+k)!(s-k)!
n! |
|
|
| = |
(-1)n+k+l(-s+k+l-1)!(s-k)!(s-l)!
(-r-1)!n! |
(3.2) |
|
It is plain that
is symmetric in k and l. However, the interchange of k
and l exchanges A and B, D and C, E and F.
Since A, B lie in
the same sextant, and likewise D, C and E, F, it follows
that
or
yielding a Star of David Theorem. This is truly remarkable since, from an
analytic point of view, the vertices A, B come into play precisely
when the vertices C, D are not relevant (i. e., in the expansions of
(a+b)n-k and
(a+b)n-l with |a| > |b|).It seems
that the geometry exercises a very powerful influence, blotting out any
analytic scruples.
Notice also, intriguingly, that we obtain (3.3) by cutting out the zero
factors from zero weights!
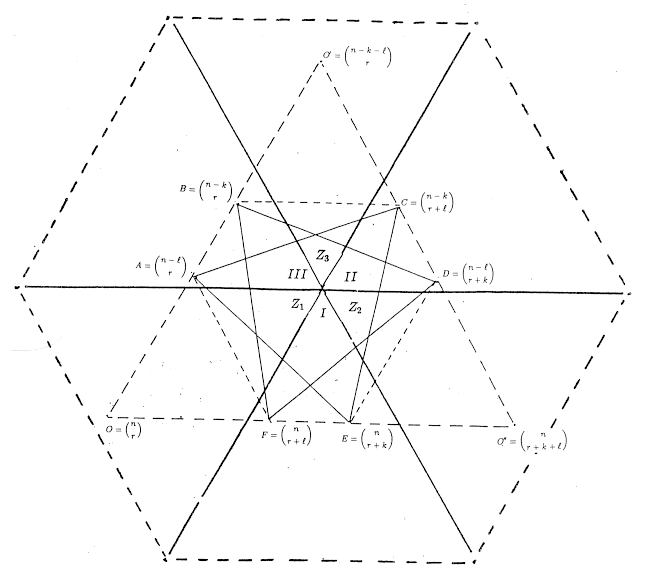
Figure 6: Unexpectedly the relation A×C×E = B×D×F survives.
4
Notice that here, and henceforth, we drop the s from the symbol
for the binomial coefficient.