|
TONAL
ORGANIZATION
Tonality and harmonic
organization are questions that should be approached from two areas: that
of "12-tone music" and that of its diametric opposite - "classical
harmony". 12-tone music confronts us with a musical ideal that seeks
to neutralize classical major-minor relationships, and be "intertonal"
1);
consequently its harmonic building blocks will be tonally neutral or tonally
indifferent equidistant chords (chords of equal pitch division)
and their combinations, namely the circle of fifths or fourths:
| and the equidistant
divisions of the octave: |
c
|
-g
|
-d
|
a
|
-e
|
-b
|
-f#
|
-c#
|
-g#
|
-d#
|
-a#
|
-e#
|
-b#
|
| the augmented
fourth chord |
X
|
-
|
-
|
-
|
-
|
-
|
X
|
-
|
-
|
-
|
-
|
-
|
X
|
| the augmented
triad |
X
|
-
|
-
|
-
|
X
|
-
|
-
|
-
|
X
|
-
|
-
|
-
|
X
|
| the diminished
seventh chord |
X
|
-
|
-
|
X
|
-
|
-
|
X
|
-
|
-
|
X
|
-
|
-
|
X
|
| the whole-tone
scale |
X
|
-
|
X
|
-
|
X
|
-
|
X
|
-
|
X
|
-
|
X
|
-
|
X
|
| the chromatic
scale |
X
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
Let us examine
more closely in what manner the vocabulary of equidistant chords forms
itself into the organic tonal system, which provides the harmonic
unity of the Sonata for Two Pianos and Percussion, and of Bartók's
music in general.
In the list given
above, the only item which embraces the whole chromatic scale is the circle
of fifths or fourths. One of the nearest natural harmonics, the perfect
fifth, together with its inversion, the perfect fourth, is treated
by Bartók - perhaps due to the influence of folk music - as the
"queen" of intervals. Following these considerations, and the lessons to
be drawn from analysis, the foundation of the present theory will be the
"tonal compass rose" - the circle of fifths or fourths.
The augmented
fourth (=diminished fifth) provides the constituents of the diminished
seventh chord, while the whole-tone scale - lacking as it does possibilities
for combination 2) - proves to be impotent
as a form-creating element; the main components of a system based upon
the circle of fifths or fourths will therefore be primarily the augmented
triad, and the diminished seventh chord. Let us see how!
A precondition
of any system of tonality is a central point in relation to which others
are dependent or subordinate. In the Sonata for Two Pianos and Percussion,
the tonal system's central point c offers itself for the role of
the
"ruling" tonic note. If we set beside it "ministers" - on the right side
a note with positive tension, on the left side a note with negative tension
- then we have already simplified the question of the governement of the
circle of fifths. Suitable for just this purpose is the equidistant
tripartite division - ab-c-e
- of the circle of fifths, the
only question being what function we should apportion to the notes e
and ab. If we look at the practice of
European music, then e, the major third above the tonic, may with
impunity be considered a dominant, and similarly ab, the major
third below the tonic, a subdominant. Even in classical harmony we find
these are lent a similar significance.
3)
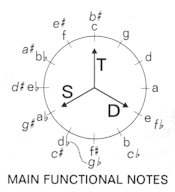
Now we shall examine
how the influence of the main functional notes - the tonic c,
the dominant e, and the subdominant ab
is
distributed. If we proportionately divide the 12 tones of the chromatic
scale between the 3 main functional notes, then each function acquires
4 "poles". The only arrangement of these poles that serves our ends,
is to quarter by equidistant division
the circle of fifths - thereby
matching the "intertonal" musical ideal of 12-tone music - in which case
we arrive at diminished seventh chords.
The following
can therefore be affixed to one another:
the diminished
seventh chord c-eb-f#-a
to
the main note tonic c;
the diminished
seventh chord e-g-bb-c#
to the main note dominant e;
the diminished
seventh chord ab-b-d-f
to the main note subdominant ab;
this especially when
we consider that the tonic character of c and a
(degrees
I and VI), the dominant character of g and e (degrees
V and III) and the subdominant character of f and
d
(degrees IV and II) agree with the principles of classical harmony.
On the other hand we have satisfied the requirements of 12-tone music by
each of the above listed "tonally" joined notes c-a, g-e,
f-d,
being neutralized by its "counterpole" - slicing diagonally the
circle of fifths - for example c is neutralized by f#.
This same result
can be arrived at based upon another theoretical consideration as well.
Taking note of the fifth-fourth attraction that binds the tonic to the
dominant (V-I), the dominant to the subdominant (secondary dominant), and
the subdominant to the tonic (I-IV), thus regarding Bartók's 12-tone
musical functions based upon the circle of fifths or fourths, we see the
following system:
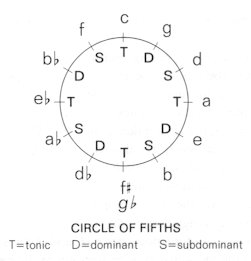
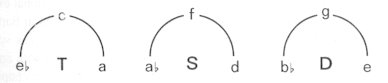
If c is
therefore regarded as the tonic, f (degree IV) as the subdominant
and g (degree V) as the dominant, then a (as relative to
the tonic) will have a tonic significance, d (as relative to the
subdominant) a subdominant significance, and e (as relative to the
dominant) a dominant significance. The circle of fifths segment f-c-g-d-a-e
is, therefore, matched by the set of functions S-T-D-S-T-D. In this relationship
a certain regularity is to be observed, as the S-T-D periodically recurs.
In essence the above diagram does no more than extend this S-T-D attraction
to the whole circle of fifths!
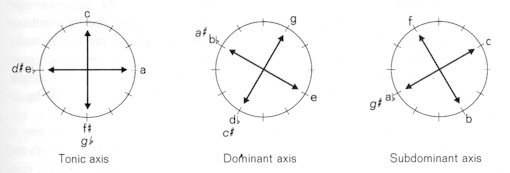
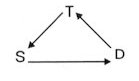
The clearly defined
separate levels of the tonic, dominant and subdominant "axes" (to
coin a name, lacking terminology) remain either practically intact,
or are interrupted by an answer at the fifth during their participation
in the overall formal structure.
Within
each axis, viewed as a unified harmonic plane, the tonal tension produced
may be of two kinds:
1. Tension
between the opposing pole and counterpole. By counterpole is meant
the note of the pole in the circle of fifths that at the same time splits
the octave in half, e.g. c and f#. This pole-counterpole
relationship should be regarded as one of the most fundamental formal principles
of the Sonata. A basic tenet of the axis system theory is that the
pole may be exchanged at any time for its counterpole without a change
of function. (A cadential harmonic progression E-A-D-G-C-F in Bartók's
system can, for example, be conceived as follows: E-A-Ab
-C#-C-F, in which the d and g are replaced by ab
and
c#.)
2. Tension
between the opposing main-branch and sub-branch. The "main-branches"
- in the diagram (Figure 3) - are the lines joining the counterpoles of
the main functional notes, that of the tonic axis being c-f#, that
of the dominant e-bb,
and of the subdominant ab-d.
(For this reason the terms "Bartók dominant" and "Bartók
subdominant" are used in this analysis to mean e or bb,
and
ab
or
d, respectively.) The
"sub-branches" intersect the main-branches at right angles, that of the
tonic axis being a-eb
, that of the dominant
g-c#,
and of the subdominant f-b. 4)
It is essential
that the individual axes be seen not as diminished sevenths, but as the
synthesis of two tritone relationships, i.e. as a scheme wherein the "opposite"
sides react to each other more sensitively than the "neighbouring" ones.
The differentiation between the main-branch and the sub-branch became necessary
not just systematically. We shall see how the "Bartók dominant and
subdominant" are given a much more emphatic role than the classically understood
dominant and subdominant. For example, in movement I a powerful appearance
of the tonic c is almost always preceded by the tonality of bb.
5)
A dominant-tonic
resolution, therefore, may be the following - in the tonality of c -
based on the possibilities inherent in the axis system: G-C, E-C, Bb-C,
the fourth and last being C#-C; that is to say, in the axis system
a dominant of C is also C#. This resolution is reserved by
Bartók for occasions when something unexpected takes place, such
as a change of scene. The explanation for this is that after C#,
cadentially we expect F#, whereupon the F# is surprisingly
exchanged for its counterpole, C, the expected C#-F# being
resolved instead by the "Bartók deceptive cadence",
the progression C#-C, (cf. Music for Strings, Percussion and Celesta, movement IV, bs.
73-74, 98-99, 113-114, 243-244).
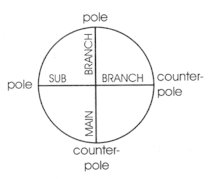
The constituents
of the axis system, therefore, are:
| the "pole" itself |
- (without dimension) |
| pole + counterpole
= "branch" |
- (1 dimensional) |
| main-branch +
sub-branch = "axis" |
- (2 dimensional) |
| T + D + S axes
= "axis system" |
- (3 dimensional) |
Unquestionably,
the instrumental combination of the work, with the neutral sound of the
percussion, provided a very attractive opportunity to thoroughly put into
effect a tonal conception of this nature.
The minor third
intervals that lie between the poles of a particular axis can best be compared
to the relative major-minor relationship in the classical harmonic system.
Nonetheless, the concept of "tonic", "subdominant" or "dominant" axes does
not accord with the similarly named concepts in classical harmony. Thus
the dominant axis resolves onto the tonic not via a leading note, but upwards
via a dorian leap of a major second (often to be observed with the progression
bb-c),
or downwards via a phrygian leap of a minor second (db-c).
In contrast to the classical dominant-tonic relationship (i.e. T-S-D-T),
the axis system often follows the plagal succession subdominant-tonic (i.e.
T-D-S-T).
The extraordinary
tension of Bartók's tonal system is very much connected to the fact
that it arises as a struggle between two spheres of opposite attraction:
major-minor tonality (the tonality of diatonicism) and the axis system
(the tonality of chromaticism).
If we look back
at the history and development of harmonic thinking, then we are bound
to say that the birth of the axis system was a historical necessity,
signifying the logical continuation of the development of Western music
and to some extent its climax. At the beginning of harmonic thinking, a
tonic, subdominant or dominant significance was clearly ascribed only to
degrees I, IV and V of the scale. Classical harmony began to include primary
and secondary triads, degree I being replaced by the relative degree VI,
degree IV by the relative II, and degree V by the relative III. Romantic
harmony went even further, making extensive use of the upper relatives,
for example in the tonality of C:
| as tonic |
c-a-eb |
| as subdominant |
f-d-ab |
| as dominant |
g-e-bb. |
From here it is
but a short step to the system "closing up": the axis extends the employment
of relatives to the whole system, since f# is a relative common
to the tonics a and eb,
b
is a relative common to the subdominants d and ab,
and c# is a relative common to the dominants e and bb.
The functional principle remains unchanged by all this; it is simply that
the number of juxtaposed planes has increased and become more diverse -
thanks to the twelve tones. Bartók's harmonic system, therefore,
is not a resumption or a new departure, but a climax and a fulfilment
(indeed historically speaking, the axis theory has a certain retrospective
aspect for musical research). Here a distinction must be drawn between
Bartók's dodecaphony and Schönberg's "Zwölftonmusik".
Schönberg demolishes and annihilates tonality, while Bartók,
with heroic effort, amalgamates the principles of harmonic thinking into
what is so far the most exquisite and perfect synthesis, one which matches
the technical standards of the times.
Here we must also
touch upon the acoustic interpretation of the axis system. A proviso
of moving from the dominant to the tonic is that we move from a harmonic
to the fundamental. According to this, the dominant of c
will be not only g, but also e and bb; it was precisely
these that went to make up earlier the dominant axis main-branch.
And because the
| D-T relation
corresponds to the |
| T-S and |
| S-D relations, |
then e and
bb will
be the dominants of the tonic base note c,
c and f#
will be the tonics of the subdominant base note ab,
and ab
and
d
will be the subdominants of the dominant base note e:
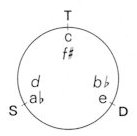
If to this we
add the role played by the harmonic at the fifth, then from these relationships
the complete axis system can be demonstrated.
An undeniable
prerequisite of an "axis-like" organization of the tonal system was the
given nature of musical feeling in general, and the fact that Bartók's
ideas derived from the best traditions, not just regarding their theoretical
organization and execution, but - what is even more significant - their
meaning and content as well. At this point the revolutionary endeavours of Liszt
and Moussorgsky come to mind; the pieces by Liszt built from perfect
equidistance - unfortunately little known - and the "axis system"
experiments of Moussorgsky. Without exception, all of these, from the "Nuages
gris", "Unstern", "Preludio funebre", death music ("R.Wagner. Venezia")
and ghostly "Funeral gondolas" of Liszt (all late piano pieces) to the
Mad Scene from Boris Godunov (pure axis system), reflect the negative side
of life - dark, demonic and irrational experiences. These ideas, either
consciously or unconsciously, also find expression in Bartók, in
that for him, chromaticism (12-tone music, equidistance, the axis
system) is synonymous with a demonic and irrational world, while diatonicism
is associated with an optimistic and bright one - a subject returned to
and further demonstrated in the chapter entitled "Meaning".
To summarize,
therefore: the above tonal system of Bartók has been shown from
four different perspectives: 12-tone music (symmetrical divisions
of the system), classical harmony (functional relations), the historical
development of music, and acoustics. That in every case these result
in a congruity of means, shows that Bartók, when he created his
musical material, penetrated to the roots of music, to its most inherent
elements. Everything that was true he recognized as the truth, and out
of these truths he created a most exquisite unity. Before dealing further
with a demonstration of the axis system, we must turn our attention to
a number of matters concerning Bartók's use of proportion.
* * *
It is suggested
that the reader, before commencing any detailed dissection, should study
the extracts below on the basis of the present analysis: movement II
bs. 5-13 and 48-56, movement I bs. 61-68, 195-216, 232-247, 417-443.
1) Lendvai
here coins a new term, "hangnemközi". The Hungarian means literally
"between keys", translated here as intertonal (remark of the translator).
2) As
the combination of two whole-tone scales produces the chromatic scale.
3) E.g.
the first half of the development section of movement I falls under the
E dominant (161 -) and the second half under the G# subdominant (217 -).
A similar structure is also revealed by the second subjects of movements
I and III:
movement I from 84 is in E, from 95 in Ab
movement III from 44 is in E, from 74 in G#
Further good examples
are the sequence of tonalities in the Rondo in C major (C - E - Ab-
C) and movement I of the Concerto for Orchestra: Exposition in F (76),
Development in Db
(231) and A (313), Recapitulation in F (386). In Beethoven's sonatas
the dominant second subject often appears on the upper third of the
keynote (e.g. the C major Waldstein Sonata's second subject in E major),
and the subdominant slow movement on the lower third of the keynote (e.g.
the C minor Pathétique Sonata's Adagio in Ab).
The sequence of keys in Brahms' First Symphony is: movements I and IV in
C minor and major, movement II in E major, and movement III in Ab
major.
4) Cf.
movement I bs. 235 - 247: placed opposite the subdominant d - g# main-branch
(bs. 239 - 241) is the f - b sub-branch (bs. 244 - 247); bs. 417 - 443:
the first section instead uses the tonic eb-
a sub-branch (417 - 432), while the second section uses mainly the c -
f# main-branch; the outer sections of movement II are based upon
the subdominant axis b - f sub-branch, and the middle section on the d
- g# main-branch, etc.
5) The
bbb
chord, introduced later on.
NEXT
Contents
|