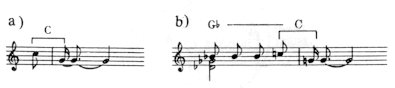|
In European music, functional way of thinking has been established with the recognition of I-IV-V-I affinities:
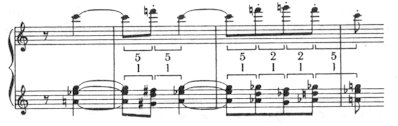
The classical theory already distinguishes between primary and secondary triads – in so far as the I, IV and V degrees may be substituted by the relative VI, II and III degrees respectively:
Romantic music continues with this progression, naturalizing the upper relatives, too:
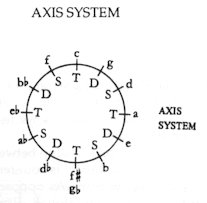
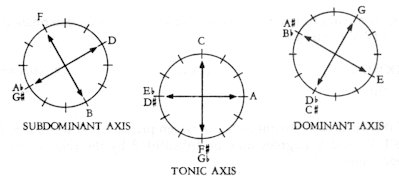
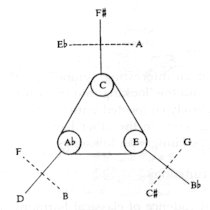
Axis system is none other than the recognition of the fact that the tonic A and Eb (see sketch above) not only have C as a common relative, but also the F# or Gb degree. Likewise the common relative, between the subdominant D and Ab is not only F, but also the B. Finally, G and C# (or Db) equally the common relatives of the dominant E and Bb degrees: Fig. 1
A backward glance at the past and the progress of European harmonic thinking gives evidence to the fact that the birth of the axis system was a historical necessity. As compared to the past, the advance consisted mainly in Bartók’s having extended these functional affinities over the entire twelve-tone series – and with this, he brought the system to a ‘close‘. We call it the axis system because in this system the opposite poles – counterpoles (C and F#, for example) – are more directly attached to each other than the relative keys of classical harmony.
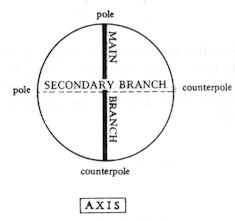
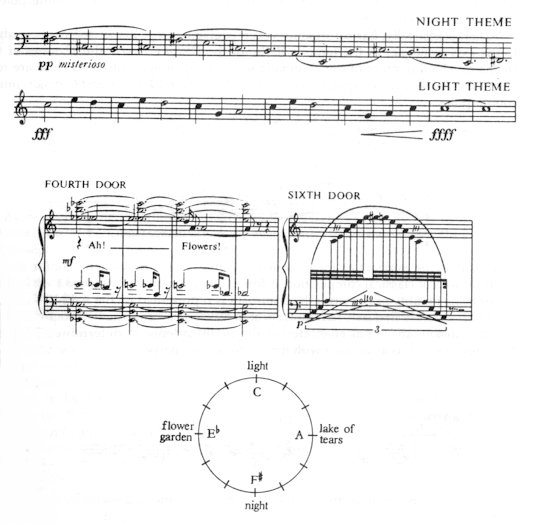
Naturally, the poles of the individual axes should not be regarded as diminished seventh chords – but as the kinship, the functional attraction among four different tonalities, similar to the relative major-minor keys in classical harmony (such as C major–A minor, or C minor–Eb major). In Bartók’s Bluebeard’s Castle the relationship between the four poles is elucidated by the scenes of the opera: the ’night theme’ is counterbalanced by the ’light theme’, and the flower-garden by the lake of tears. As opposed to the ’intellectual-spiritual’ dimension of the main branch, the ’emotional’ dimension is represented by the secondary branch: Fig. 3
Each movement of Bartók’s Music for Strings, Percussion and Celesta follows the same pattern (see: p.59). The counterpole tension became the most fundamental
Bartók’s Allegro Barbaro is based on the polarity of F# minor and C major: Fig. 4
The F tonic of the Divertimento turns into the B counterpole in the middle-part (b. 80). Likewise, the B tonic of the Violin Concerto is substituted for the F counterpole in the development (b. 115). Characteristically, Bartók organizes even twelve-degree "Reihe" themes according to the axis principle. In the famous Reihe of the Violin Concerto the 12 tones of the theme touch all degrees of the chromatic scale. Its opening, centre and close are roo-ted in the A-D#-A counterpoles – crossed by the broken F# major and C major–minor counterpoles: Fig. 5
Since this Reihe appears as the ’secondary theme’ of the movement, conforming to the traditions of classical composition, a dominant significance is attached to it: in the B major basic tonality of the work the dominant is represented by the A-F#-D#-C axis. We frequently find axis harmonization in folksong arrangements, too. In Kodály’s Székely Lament, the tonal character of the main cadence is determined by the C fourth-step which is associated with the Gb major counterpole: Fig. 6
This Gb major is coloured by the relative Eb minor, and answered by the A major counterpole. Fig. 7
A pole can be replaced by its counterpole without any change in its function. The first strophe of the above folksong ends in A7, but the third strophe closes with the Eb7 counterpole. Fig. 8
Especially in their variational works both masters exploit
to the utmost the potentialities of axis-replacement: in the newer
and newer variations they freely interchange chords belonging to the same
axis (function).
The frequent occurrence of tonal answers and tonal correspondences in Kodály’s and Bartók’s music bear witness to a distinctly functional thinking. Chiefly those countermovement chord progressions are to be mentioned which rest not on ’real’, but on ’tonal’ reflections. In the axis system, the same function can be attained by a major second step in one direction, or by a minor second step in the other. (E.g. departing from the G dominant, we reach the subdominant either with a major second step downwards or a minor second step upwards: F or Ab). As this is pictorially reflected in the ’bridge motif’ of Bartók’s Cantata Profana (’Coming by a foot bridge saw’): Fig. 9
But this rule can be extended: by moving a major second, fourth, minor sixth or major seventh interval in one direction – or by moving a minor second, major third, fifth or minor seventh interval in the other direction, we arrive at the same function in the axis system. This principle permits much bolder counter-movements too – as the Entry of the Emperor and the Imperial Court from Kodály’s Háry János indicates: Fig. 10
* Mention must be made of the apparent contradictions existing between the seven-degree and twelve-degree systems. (a) According to Riemann, the diminished triad on degree VII (B-D-F) is but an incomplete dominant seventh chord (G-B-D-F). Degree VII will have an independent function only if a major (or minor) chord is built upon it. In this case it acquires the significance of the SUBDOMINANT. Fig. 11
In classical music, the VII. degree major chord strives to resolve on III – consequently, it has a ’secondary dominant’, i.e. subdominant meaning. Fig. 12
The ambivalence between 7-degree and 12-degree music is conspicuous also in that the cadential sequence of chords
suffers a break between the F and B in the diatonic scale (a diminished fifth appears instead of a perfect fifth). Naturally, no such break occurs in the 12-note system. (b) According to Rameau, the Neapolitan sixth cannot be regarded as a real chord on the II. degree. In C tonality, the Neapolitan F-Ab -Db is not a triad based on Db, but an altered IV. degree. This is why a ’subdominant’ sense has been attached to it. – In Romantic harmony, however, the minor second degree (Db) is granted an independent role and thus it receives a DOMINANT significance (see also pp. 92-93). It is as much as saying that there is no contradiction between traditional harmony and the axis system. * Perhaps the most specific characteristic of the axis system is that the individual harmonic functions receive a symbolic meaning. In traditional music, too, subdominant was identified with the image of ‘sinking‘, and the dominant with that of ‘rising‘ – but there the various functions were dependent primarily on the circumvolution of chords (I-IV-V-I, for example). Bartók and Kodály, however, go much further and invest the individual functions with independent meaning: their content is determined by their absolute relation to the tonic axis. Examining the interaction between material and poetic content, a leading role can be attached to works with a plot or text. It can be assumed that it was in the opera genre that the ’individuality’ of the three harmonic functions developed. For example, the twelve chimes from Verdi’s Falstaff (see Fig. 160 on p.86) could scarcely evoke — without the SUBDOMINANT atmosphere belonging to it — the secret mysterious shivering which the word "mezzanotte" (midnight) expresses. On the other hand, Verdi elevates us into the sphere of the DOMINANT when he wants to portray the ’heavenly’ beauty of his female characters, or the magic of nature. The Aida-theme itself — although we are in no doubt as to its tonality — does not even touch the tonic: it floats on the fifth (and major third) of the root. (See Fig. 171 on p. 91) On Mozart’s opera stage, the mirror of the ’inner’ stage is the subdominant, and that of the ’outer’ stage the dominant. Two brief examples from The Marriage of Figaro. The outer action (which can be clearly seen ’by everyone’) is accompanied by dominant-tonic harmonies; but when the characters begin to be ’secretive’, or speak ’to themselves’, the function immediately changes to the subdominant. Fig. 13
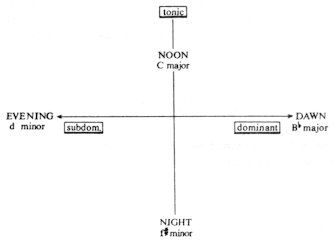
The more complex and refined individuality a Mozart figure has, the more powerful role is assigned to the subdominant function: the frequency of the subdominant is the sign of a rich ’inner life’ (as with Don Ottavio or Tamino). And conversely, the dominant and tonic gain the upper hand in the melodic world of his popular, peasant characters (like Leporello and Papageno). In Bartók’s Bluebeard’s Castle this functional ’sign-language’ goes hand in hand with the libretto. The static pillars of the opera and the points of rest are based on the tonic. The subdominant function has a negative significance, it is reserved for the burning, shapeless passion; on the other hand, every positive ’initiative’ sets out from the dominant (the possibility of elevation also resides in it). The scene of Door VII — women of the past — is particularly illuminating in this respect, with its almost cosmic arrangement of ’dawn–noon–evening–night’. In accordance with the basic idea of the work, ’night’ is identified with the tonic F#, and ’noon’ with the counterpole C. ’Dawn’ looks towards the rising dominant, and ’evening’ towards the sinking subdominant. The Bb major tonality of ’dawn’ and the D minor tonality of ’evening’ occupies a symmetrical position – whether in relation to F# or C. And again, in contrast to the major tonality of ’dawn and noon’, the harmonies of ’evening and night’ are minor in character. Fig. 14
Mention must be made of an interesting symbolism: the
‘looking towards the past’ face of the subdominant and the ’looking into
the future’ aspect of the dominant – which is, on the one hand, closely
connected with the subdominant character of the ancient six-four type folksongs
and, on the other hand, with the T-D-D-T (T-T-D-T) cupola structure of
the new-type Hungarian folksongs.
The relationship of the three functions As opposed to the I-IV-V-I cadence of classical harmony, the tonic, subdominant and dominant functions are most powerfully represented by the three degrees which divide the fifth-circle into three equal parts – thus constituting an augmented triad relationship. For example C-E-Ab, in the sense of tonic, dominant and subdominant. This is, after all, nothing new. The movements in Brahms’ First Symphony follow each other in this way: C-E-Ab-C, in the sense of tonic-dominant-subdominant-tonic. The dominant secondary theme in Beethoven’s C major (Waldstein) Sonata appears in E, and the subdominant slow movement in the C minor (Pathétique) Sonata in Ab major. The first movement in Bartók’s Concerto for
Orchestra rests on the five-fold appearance of the principal theme:
A similar order of keys can be observed in the First Rondo for Piano: C tonic, E dominant, Ab subdominant, C tonic. The tonal arrangement in Movement I of Bartók’s
Sonata
for Two Pianos and Percussion is as follows:
Each axis contains in itself a double attraction, a twofold dimension – depending on whether we contrast the pole with the counterpole, or the ’main branch’ with the ’secondary branch’ (see: Fig. 2 on p. 8) which means that the individual axes divide the fifth-circle into four equal parts. All in all, the tonal system created by the equal divisions of the circle of fifths matches the model of the axis system: Fig. 15
Therefore, the constituents of the axis system are:
It is easy to understand that — given three functions
— only one tonal system can be established by the distance divisions
of the circle of fifths, and this is identical with the axis system.
Tonal ’asymmetrical’ and atonal ’symmetrical’ elements It would be tempting to speak of ’relativity theory’. The axis system preserves tonal — and indeed, functional — thinking, but at the same time it also satisfies the distance laws of twelve-tone music. It represents an order which results from the meeting of opposites. In this respect, too, the two Hungarian masters continue one of the most peculiar traditions of European music: they ’re-live’ in a condensed form the historical progression which (with the advance of distance models and their gradually increasing conquest) finally led to the free and equal treatment of the twelve chromatic notes. It was exactly in the interaction between tonal ’asymmetrical’
and atonal ’symmetrical’ elements that the harmonic world of European music
became a dialectic lingual system. In the antagonistic features
of the axis system, actually, the inherent contradiction between tonal
and distance principles is reflected.
|