|
'We are guided by nature in composition'
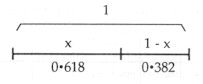
Golden section (sectio aurea) comes about when the proportion of the whole to the larger part agrees with the proportion of the larger part to the smaller one. That is, the larger part becomes the geometrical mean of the whole distance and the smaller part. Practically, if the whole is considered as 1, the value of the larger section will be approximately 0.618 and that of the smaller section 0.382. Fig. 16
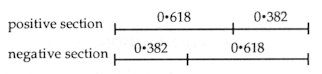
From a structural aspect Bartók's greatest works are the true representations of the golden section principle - frequently from the whole form down to the smallest form-cells. For example, the first movement of Sonata for Two Pianos and Percussion consists of 443 bars. If 443 is multiplied by the key-number of the golden section (i.e. 0.618), we get 274, and indeed, b. 274 marks the 'centre of gravity' in the form: the entry of the recapitulation. The complete form of Sonata for Two Pianos and Percussion consists of 6432 eight notes. In compliance with the form construction of the work: slow-fast + slow-fast movements, its golden section - 3975 eight notes - touches the beginning of the second slow movement. The first movement in Bartók's Contrasts comprises 93 bars. Its golden section - 93-times 0.618 - coincides precisely with the recapitulation (at the middle of b. 57). The first movement of Divertimento contains 563 triplet units (because of the varying time-signatures we have nothing to do with the number of bars), and its golden section - 563-times 0.618 - once more agrees with the recapitulation. At a cursory glance it may seem illogical that the change in tempo does not influence the position of section points. The contradiction, however, easily disappears if we realize that the 'heartbeat' of music is the metrical pulse, and not the absolute length of time measured by the clock. In music, the progress of time is indicated by bar-lines or rhythmic beats - and the role of these metric impulses is more vigorous and emphatic than the space of time in which the music takes place. Subjectively time progresses more feverishly with fast beats, and more restrained in a slow pulsation. Golden section has two possibilities: a 'positive' and a 'negative' - depending on whether the larger part precedes the shorter, or vice-versa (long+short part provides a positive, and conversely, short+long a negative section): Fig. 17
A fine example of the extent to which golden section proportions may dominate melodic structure, is reflected by the 16 introductory bars of the first movement of Bartók's Sonata for Two Pianos (or to be more exact, bs. 2-17, since the organic life of the work is developed from b. 2 onwards). Fig. 18
This is what happens:
Similarly to classical period, positive and negative sections create questions and answers. Both in the larger and the smaller details questions and answers, that is positive and negative sections unite symmetrically - in such a way that the smaller form-units are finally merged in a positive main section. This is why the form is associated with a dynamic rise, from pianissimo to forte-fortissimo! We may draw the inference that positive sections are accompanied by a dynamic increase, the intensification or condensation of the musical material (i.e. question), and conversely, negative sections go hand in hand with a downward tendency, decline, lose of strength (i.e. answer, release). From these analyses it can be seen that the golden section meets, in every case, the most important turning point of the form. It goes without saying that golden section appears not as a mathematical rule - it were useless to seek a mathematical logic in these structures. It may be added that in Bartók and Kodály's 'asymmetrical-polyphonic' way of writing, it is not the number of bars but the number of musical impulses that determines the proportions. To give a typical example, at the very end of the Fourth Quartet (from b. 365 on) it can be clearly perceived that 3 motivic 'waves' are answe-red by 5 motivic waves (bs. 365-374 and 375-385). Or in the Háry János Prelude, the 4-fold entry of the principal theme is responded by 6 theme-entries (regardless of the distance between the individual entrances). Accuracy controlled by perception and accuracy tested by calculation are two sides which must be kept distinct. I discovered golden section intuitively and empirically: my observations were founded on real experience. Where does precision end and inaccuracy
begin? I would propose that:
Golden section is subject to three conditions.
Golden mean is no more than an organic element of the musical dramaturgy and has a meaning only in relation to the contents of music. The point of our interest is first of all the 'effect mechanism' of the proportions: the attractive and repelling force functioning in the positive and negative sections, the interaction between the building elements. * 'Two elements cannot be well coupled without the assistance of a third one, since the two can only be united by an intermediary link; but of all the links that one is the most beautiful which unites into a complete whole itself and the elements joined by it.' (Plato: Timaeus) The static quality, classic beauty of Parthenon in Athens may be attributed to the fact that into its forefront - between the base and the tympanon - exactly two squares can be inscribed. On the other hand, its dynamic quality - the floating effect which invisibly draws the building upwards - is due to the golden section proportions. We give the structural view after Zeising (see next page). Perhaps the most beautiful literary manifestation of the golden section principle is Dante's Divine Comedy. The golden section of the hundred Cantos comes at the end of the sixty-second Canto: this is the point where Dante parts with Virgil and continues his way with Beatrice. From here (Purg.XXVIII) the language, the colour, the tone and even the atmosphere of the work change. The great physicist Einstein, too, pronounced in favour of the golden section. According to him, golden section provides a proportion which throws difficulties in the way of the bad and facilitates the development of what is good.
A pair of compasses can be seen in the Neapolitan museum which served for measuring the golden section in antiquity:
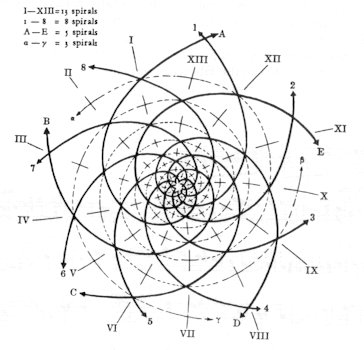
The Fibonacci series covers the simplest golden section sequence which can be expressed in whole-numbers (the golden section of 89 being 55, and that of 55 being 34, etc.): 2, 3, 5, 8, 13, 21, 34, 55, 89 ... In it each number equals the sum of the two preceding numbers (that is, 2+3 =5, 3+5=8, 5+8=13, etc.). The sequence approaches nearer and nearer the proportion of the geometrical golden section i.e. the irrational key-number of the geometric mean: the square of every number is equal to the product of the numbers preceding and following it - with the difference of plus or minus 1. The Fibonacci series embodies the low of natural growth. In the fir-cone starting from the centre, a system of spirals runs in the right and left directions, in which the number of spirals always result in the values of the Fibonacci sequence: 3, 5, 8 and 13 spirals.
A similar setting can be seen on the sunflower, pineapple, chamomile, dandelion, marguerite, cactus, likewise in the arrangement of leaves on the stem, in the horns of some ruminating animals - to mention only the most characteristic examples. Bartók adopted this numerical series already at the beginning of his career, in 1911. The throbbing F # minor ostinato of Allegro Barbaro appears in groups of 3, 5, or 8 or 13 bars. Perhaps the most beautiful musical representation of the Fibonacci sequence is the first movement - the 'pyramid-fugue' - of Music for Strings, Percussion and Celesta (for a detailed analysis, see pp. 56-65). Golden mean is not merely an important factor of form and structure, but it gives a key - almost a solution to the question of tonal and harmonic structures as well. And this is no casual coincidence. The most elementary musical expression of the golden section principle is pentatony itself. When a child sings the simplest pentatonic phrases, he instinctively does nothing else than 'tunes' the motif to the proportion of the golden section, i.e. the geometric mean. Fig. 21
Calculated in semitones, the formula of the LA-SO-MI motif is 2+3=5; by adding also the upper DO to it, a distance of 8 semitones issues which shows a subdivision of 5+3 and 3+2+3. 'Folk-music is a phenomenon of nature... its formations have developed with the same organic freedom as other living organisms: the flowers, animals...' - Bartók once declared. In the first movement of Sonata for Two Pianos and Percussion each new theme-entrance rises one step higher in the Fibonacci sequence: Fig. 22
The harmonic structure of the exposition gives proof of a similar arrangement: each new harmony advances one degree in the golden section scale: Fig. 23
The closed quality is one of the distinctive marks of golden section forms. This world of form has a peculiar glow - a life-tension and an organic closedness - and this is a direct consequence of the fact that evidence of golden section structures is found only in living organic nature, but it is quite alien to inorganic nature, to the world of crystal forms. (See also Fig. 58-59 on pp. 37-38)
*) For detailed analysis see: Ernő Lendvai: The Workshop of Bartók and Kodály, Editio Musica, Budapest, 1983, pp. 36-40
|