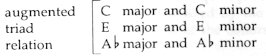|
PRINCIPLES
The harmonic types of the chromatic system,
that is
are characterized by the fact that they unite the tension of the Fibonacci-models with the closedness of the twelve-tone system. The most characteristic chromatic melodies
and harmonies obey the proportions of the Fibonacci sequence. Calculated
in semi-tones:
In reality, these numbers express proportion
and not semi-tone steps.
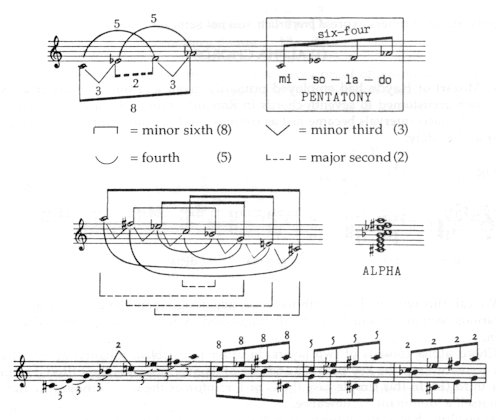
As Mozart or Haydn had employed primarily major and minor triads or as we had grown accustomed to seventh-chords in Romantic music, the use of harmonies built of Fibonacci intervals became just as common and predominant in the works of Bartók and Kodály: Fig. 24
We call this type of chord with the collective designation: the alpha harmony — the various sections of which can be distinguished by letters beta, gamma, delta and epsilon. Chord alpha consists of two layers. In order to establish tonality, at least two notes are necessary: the key-note (C) and one of its overtones: i.e. the fifth (G) or the major third (E). In this simple case the G or E reinforces the C — although G and E has in itself a ’dominant’ significance. Type alpha has a strong tonal, even functional character. When, for example, in the main cadence of the ’Recruiting Music’ Kodály looks for a dominant alpha chord (before the tonic E major), he moulds its upper layer from the melody itself (B-G#-F-D), and the lower layer from the diminished seventh chord C-D#-F#-A: Fig. 25
Thus type alpha is nothing less than the ’axis’ adaptation of the simple C-E-G or C-G relation (this is why type epsilon rarely occurs owing to the absence of the fifth and major third – G and E – without which the tonal character of the chord is unsteady); the sole requirement is that the chord should be constructed of two layers (two ’axes’). Type alpha complies with two requirements. On the one hand it derives from pentatony. The intervals 2, 3, 5, 8 (or their octaves) sound together with every note of the chord. Fig. 26
This is how in one of Bartók’s choruses the pentatonic DO-SO-LA-MI motif is transmuted into gamma and delta harmonies: Fig. 27
On the other hand, alpha harmonies are axis models and, as such, express the polymodal tensions of the axis system. (See: Fig. 32 on p. 27) Let us add: the tension of alpha harmonies may — most simply and effectively — be expressed by the symbols of polymodality. Fig. 28
Examples Fig. 29.
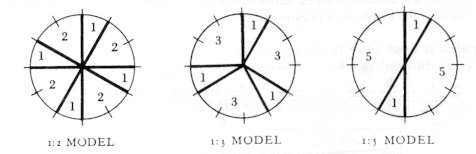
By the chromatic juxtaposition of intervals 2, or 3, or 5, ’closed’ scales are produced (i.e. by the periodic repetition of the intervals we are taken back to the starting point). MODEL 1:2 is an infinite chain of minor and major seconds,
MODEL 1:3 is an infinite chain of minor seconds and minor
thirds,
MODEL 1:5 is an infinite chain of minor seconds and fourths,
Fig. 30
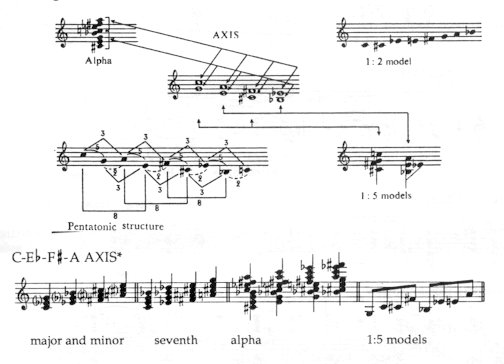
Model 1:2 should be considered the ’fundamental scale’ of the axis system. In the 12-note system three different 1:2 models may be established, in accordance with the three functions: a tonic, a dominant and a subdominant. Every further form agrees with one of these models, e.g. in C tonality: Fig. 31.
All chords and models appertaining to the same axis constitute a functional unit.
Examples Fig. 33
1:2 model harmonic turns **) If we combine a major seventh and a subminor chord — lying a minor third higher — we get the 1:2 model. This combination became current among the Romantics. Fig. 34
In Act I of Tristan, the ’inner’ world is visualized by the ’Tristan chord’ (F subminor), while the ’outer’ world by the chorus of the Sailors – at all times appearing in the form of a ’D major seventh’ chord. Fig. 35
Model 1:5 represents another typical axis sequence: it rests upon polar relations. Fig. 36
Fig. 37
Model 1:2 may be split up into two 1:5 models. Fig. 38
In the Mikrokosmos piece From the Island Bali both left and right hands play 1:5 models, which together create a complete 1:2 model. Fig. 39
The closing chords unite these four elements. Fig. 40
In the final chord two triads are merged: the difference of six accidentals between the two triads create a polar tension and the two triads fuse in a perfect alpha harmony. Fig. 41
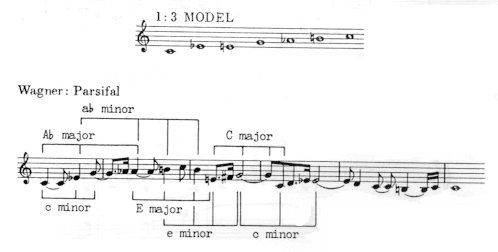
While models 1:2 and 1:5 have a powerful ’tonal’ character, the 1:3 model ’annihilates’ tonality due to its augmented triad structure. For instance, the C-Eb-E-G-Ab-B 1:3 model comprehends the following triads:
The ’floating’ quality of model 1:3 was already recognized by Liszt and Wagner.
Examples Fig. 43
Complementary (annihilating) keys A 1:3 model can be created by uniting a major and a minor triad (the latter lying a major third lower). In this case one triad neutralizes the other since their notes combine in an atonal 1:3 model. This is why such triads express a contrast in their content as well. Fig. 44.
The idea of ’annihilation’ goes back to Romantic models. When Wotan in the great Monologue of the Valkyrie prophesies the Twilight of Gods, his words "Das Ende! Das Ende!" evoke E major and C minor – which tonally destroy each other.
A peculiar manifestation of the ’annihilation’ idea is Webern’s famous Reihe – in which two 1:3 models are merged: Fig. 46
A change from major to the complementary minor (E major—C minor) results in a ’negative effect’, it is associated with gloomy, or even, oppressive and irrational experience. (See Fig. 45 above) And conversely, a change from minor key to the complementary major (e.g. C minor— E major) creates a ’positive’ impression, it is inspired by enthusiasm and serenity – like the E major episode at the end of Beethoven’s Piano Concerto in C minor. In the chorus The Aged, Kodály translates the life-and-death symbolism of the piece into the language of music by means of complementary keys: G major and Eb minor – then Bb minor and D major: Fig. 47
The entire tonal plan of Bluebeard’s Castle is built up of such complementary relations. F# minor is the key of ’night’ and C major that of ’light’. C major can be destroyed by means of the Ab minor key – thus the latter is associated with ’death’ symbolism. On the other hand, the night’s F# minor can be defeated by Bb major – thus it became the symbol of ’love’. The four triads together include every degree of the chromatic scale:
The basic tonality in Kodály’s Psalmus Hungaricus — A minor — is equivalent to weeping, imploration, despair, curse. The dénouement of the action, on the other hand, takes place in the complementary key: Db = C# major. It is the task of Db major to absolve from the weight of the curse: ’From you he removes your every burden’. And that of C# major to become the key of elevation and apotheosis: ’In honour Thou wilt raise him on high!’ Complementary keys may appear in a hidden form, too. The "Sündenqual-motiv" from Parsifal exerts a tormenting effect because the authentic sequence (moving authentically on the circle of fifths) is coloured by complementary chords: F major and Db minor in b. 1; Db major and A minor in b. 2, etc. Fig. 48
Closed sequences may, however, be created
by simpler means – by composing equidistant scales from the Fibonacci intervals
2, 3, 5, 8:
can be established.
Fourth chords**) Owing to the folksong inspiration, strikingly frequent is the theme formation and harmonisation with fourth chords. ’The characteristic fourth-accumulation in our ancient melodies spurred us on to the forming of fourth chords: we have projected here the horizontal succession into vertical simultaneity’ (Bartók: The Influence of Peasant Music on Modern Music, 1920). This is how Bartók transforms the fourth melody into a fourth harmony in the Violin Concerto: Fig. 49
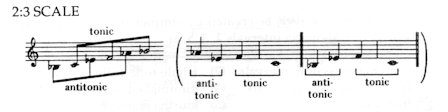
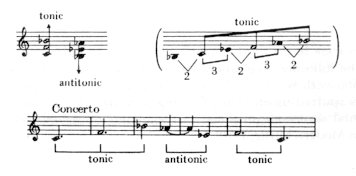
Tonic–antitonic relations in the pentatonic scale Thus, fourth chords in Bartók and Kodály’s compositions derive from folk-music, and in keeping with the folksong inspiration, also in the connection of fourth chords the inner laws of pentatony assert themselves. To mention the most important one: of two fourth chords which are placed at a distance of a minor third (3) or major second (2) from each other, the ’tonic’ model is always the one which lies a minor third lower or (which means the same) a major second higher than the other. We call one of them the ’tonic’ and the other ’antitonic’ model: Fig. 50
In Fig. below, the ’tonic’ model is represented by fourth-degrees C-F-Bb, and the ’antitonic’ by fourth-degrees Bb-Eb-Ab. Fig. 51
The tonic-antitonic attraction originates in the SO-RE’MI (DO-SO’LA) cadence so frequent in folk melodies: the SO-RE holds the tension, while the MI corresponds to the tonic resolution: Fig. 52
It deserves a special attention that this time we are faced with a two-function system (and not a three-function one, as in classical harmony). Incidentally, chords based on the SO-LA-DO-RE
structure have a floating, soaring effect since the tonic and antitonic
(RE-LA and DO-SO) relation supports not the lower, but the upper note.
In my analyses, the letter omega indicates the whole-tone scale. I have deliberately chosen the letter farthest from alpha because Bartók himself used them oppositely. Alpha is ’tense’ in character, omega is ’dissolved’ – and this quality becomes apparent in that the whole-tone scale, as opposed to alpha and pentatonic structures, contains not one single perfect fourth (nor a perfect fifth) without which the tonal character of the chord becomes unstable. In the 12-tone system two omega scales can be distinguished (6+6 notes), they are mutually ’geometrical dominants’ of each other (C-D-E-F#-G#-A# and Db-Eb-F-G-A-B): w1 and w2.
Kodály’s chorus Fancy concludes with a complete omega harmony – depicting the peal of bells: Fig. 54
The omega harmony — due to its fluid character — lends itself particularly well for tone-painting (landscape painting). We give a Kodály example: Fig. 55
Because of the contrast, the direct confrontation of the alpha and omega tonalities is very effective. In the third movement of Music for Strings, Percussion and Celesta, the central ’light’ theme — accompanied by the high-pitched cymbal — also includes this duality. The motif is ’centralized’ around the C note. Depending on whether it occurs in root position or inversion,
it can be accompanied by omega chords (Fig. 53 on p. 35) or by alpha chord: through the periodic repetition of diminished triads, a closed alpha structure is created: Fig. 57
* In practice, the Fibonacci models — i.e. alpha and axis harmonies, 1:2, 1:3, 1:5 models and equidistant scales — merge into each other. In Fig. below, the hunting ostinato is quoted from the chromatic first movement of Bartók’s Sonata for Two Pianos and Percussion:
The entire chromatic scale is included in the twelve notes of the ostinato. A pole—counterpole relationship exists between the opening and the closing notes (upper part A and Eb, lower part F# and C), forming together an axis arrangement: F#-A-C-Eb. The upper part is composed of the A-B-Db-Eb-F-G omega scale (its formula being 2+2+2+2+2+2), while the lower part of the complementary omega scale – F#-G#-Bb-C-D-E. The two parts progress in parallel minor thirds (3). Motivically, each part is built of minor sixth (8) elements: the upper part of augmented triads A-F-Db and B-G-Eb, and the lower part of augmented triads F#-D-Bb and G#-E-C (8+8+8). The harmonic character of the ostinato is defined by gamma chords (3+5+3) and 1:3 models:
The two 1:3 models can be fitted chromatically.
Thus all of the structural elements are ’Fibonacci formulas’.
The basic form of the diatonic system is the so-called acoustic scale (DO-scale with FI and TA), e.g. C – D – E – F# – G – A – Bb – C and the acoustic harmony, for example, C major triad with natural seventh Bb, acoustic fourth F#, and major sixth A (’pastoral’ sixth) – which is called acoustic since its notes originate in the natural overtone series: Fig. 60
Examples Fig. 61
Other examples see: Fig. 87 b on p. 50 and Fig. 107 on p. 65. The acoustic character becomes even more effective if it is the result of an expansion. The hunting-fugue in Bartók’s Cantata Profana becomes so explosive since the minor third changes into major and bursts with an acoustic fourth (MA-MI-FI): Fig. 62
The perfect fifth frame of the theme and its two ’points’ — the acoustic fourth at the half-close (FI) and the acoustic MI-TA step at the full close — only enhance the natural atmosphere of the scene. The acoustic chord, with the exception of one tone, contains a whole-tone scale (omega) as well: Bb-C-D-E-F#. Therefore, the acoustic chord can easily be coloured by the omega scale: Fig. 63
The acoustic harmony is familiar in Kodály’s music too – although he had an affection for the brighter Lydian modality: Fig. 64
In Kodály’s music there is often very little difference between the acoustic harmony and the polar harmony. For example, in Fig. above the first chord is the combination of Bb seventh and E seventh. The acoustic chord of Fig. 84 b consists of the C major and F# major counterpoles. Now we try to find a new path in deducing the acoustic harmony. Let us start from our observations See: p. 77 that the relative of the C major is A minor – and that of the latter is F# subminor:
The tones have a symmetrical distribution – around the virtual RE (=D) symmetry center! If we combine the tones of the three chords we obtain an acoustic harmony. In both cases FI and TA are determinants of character. And what is evident again: FI and TA are exact reflections of each other in relation to the RE symmetry center. The acoustic scale became a static ’colour chord’ because it lacks the two sensitive notes that characterize the major scale: instead of FA and TI (F and B) FI and TA (F# and Bb) notes occur. What the spectrum of rainbow-colours is
in optics, is the natural overtone scale in music. (The term ’acoustic
scale’ comes from me – 1947).
Whenever Bartók or Kodály intends to endow the acoustic harmony with more ’light’, the minor seventh of the acoustic chord is raised to major seventh. Fig. 66
We shall call this chord type (major triad with major seventh) the hypermajor harmony:
The hypermajor embodies the most solemn sound-type in Bartók and Kodály’s music (the opening chords of Psalmus Hungaricus and Budavári Te Deum are hypermajor harmonies) – it has become the characteristic concomitant of apotheoses. The origin of the well-known ’Bartók signature’ also goes back to the hypermajor: Fig. 68
The hypermajor owes its light not only to its major character and major seventh, but primarily to its consisting of two perfect fifths (see Fig. 67 above). In the most pictorial effects the hypermajor harmony merges with the acoustic fourth (FI): Fig. 69
The hypermajor has a counterpart: the hyperminor. Its construction is a minor triad with major seventh (the Eb-G-B augmented triad adds considerably to its individual colouration):
’Your leitmotif’ – wrote Bartók in a letter to Stefi Geyer. It is to be found all over where the text speaks of pain and passion (see: Fig. 70 b above). By inverting Bartók’s ’leitmotif of love’, a peculiar kind of chord arises – which in Bartók’s works is associated with the symbolism of death: ’Eros turns downwards his torch!’ Fig. 71.
It appears whenever desire is fulfilled and, as a consequence of the fulfilment, passion ceases. Through the inversion the augmented triad of the hyperminor (Eb-G-B in the foregoing example) moves to the bottom of the chord: A-F-C#; this is the source of the neutralizing effect. The final chord of Bluebeard’s Castle is also a hyperminor-inversion, the whole opera terminates in this symbol of death: Fig. 72
If it is true that the diatonic system is merely a mirror-image of the chromatic system,***) then ’diatonic’ sound-types can be produced by inverting the layers of the alpha harmonies: Fig. 73
The diatonic impression is the direct result of the alpha-inversion being ruled by fifths, major thirds and minor sevenths (i.e. the closest overtones) that are precluded by the alpha harmonies. Oddly enough, the harmony with a major third above the root and with a minor third below it, evokes the most ’opened’ impression: Fig. 74
And to bring to an end the interconnections: the alpha-inversion carries in itself the seed of the acoustic harmony as well: Fig. 75
By exchanging the C and F# notes, a polar relationship can be effected (C and F# seventh chords, or C and F# ninth chords). The recapitulation theme in Kodály’s Háry Prelude (Fig. 84 b on p. 48) may be interpreted equally as a C acoustic or an F# acoustic tonality. This 4-note polar formula started gaining ground already in Romantic music. The tonal nucleus of Station 10 in Liszt’s Via Crucis, or the fortissimo explosion introducing the great ensemble of Act III in Verdi’s Otello, allows the following interpretations: Fig. 76
*
*) It includes subminor chords, too (see. p. 77) (ed.) **) Title given by the editors. ***) (see pp. 48-50)
|