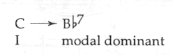|
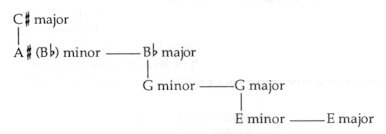
Should the modal character and — from a bird’s-eye view — the organization of the twelve solmizating letters be summed up in a few lines, it might run as follows: The twelve degrees of the chromatic scale can be arranged in three groups. First: the most peculiar feature of the system is that its center is being marked by a ’Black Hole’. The center — the zero point — coincides with the point of ’atonality’. Up- and downwards from the RE or SI (D or G#), every degree occupies a symmetrical position. (E.g., on the piano keyboard — related to D or G# — each interval has its exact mirror image). Symbolically speaking, an element that is symmetrical to everything represents the state of ’physical death’. The symmetrical division (the repeated bisection) of the circle of fifths — around the RE symmetry center — results in the ’tension’ points of the system. (See first diagram of Fig. 214 on. p. 110) Thus, if we separate these symmetry points from the chromatic scale, we arrive at the RE–SI and TI–FA tritones – creating the so-called ’sensitive notes’ of the major and minor scales (in the major: B and F – in the minor key: D and G#). However, if we omit these 4 notes from the circle of fifths, the basic scale of the ’chromatic system’ is obtained: in our terminology, the 1:2 model. Second (in fact, this should be put in the first place): the most static pillars of our tonal system are constituted by the DO-MI-SO and the relative LA-DO-MI triads (i.e., C major – and A minor belonging to it). The third group contains typical modal colours: The upward luring DI and FI produce a
chiaro
effect, whereas the MA and TA an oscuro one. But while DI and MA
(C# and Eb) appear
as tense dynamic elements, FI and TA (F# and Bb)
emerge as static colour elements. DI and MA suggest a ’major’ and ’minor’
tension, respectively. On the other hand, FI and TA determine the character
of the ’acoustic’ (overtone) scale. (Summary
on pp. 110-112)
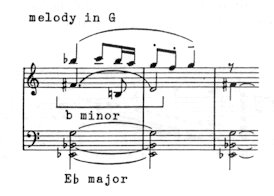
I suppose it was Verdi’s Otello which made me realize that the basic concepts of our music theory (and even the elementary particles and atoms of classical harmony: such as the images of major and minor chords fixed in our minds) called for a reappraisal, a better approach, a new interpretation. Let us set out from the Db major triad (C# in fact) which crowns the first act of Otello. Can we manage to apprehend the essence of the phenomenon if this chord is interpreted, on the basis of our classical knowledge, as a ’major chord of degree I’? In this case precisely the most important experience would be lost: the description of the unique ’elevation’ which causes the stars to light up at the end of the act ("Vien... Venere splende") and which raises the lovers into heaven. (See Fig. 109 on p. 67) If the tonic E major is regarded as a DO-MI-SO chord and the C# minor as a LA-DO-MI chord, the C# major harmony will then necessitate a LA-DI-MI interpretation! Relative solmization makes a tangible distinction between the two kinds of major triad: the E and C#. The DO-MI-SO and LA-DI-MI triads represent quite dissimilar tonal qualities, different musical ’characters’. The principal idea of the work, the ’kiss theme’, into which the end of the act flows, leaves no doubt about the basic tonality. It takes place within the compass of the 4# E major and C# minor; then after a definite cadence — with a few linking notes — it opens out in the C# major chord.
Both are ’major’ chords but because of the DI degree, the LA-DI-MI harmony is much brighter and more exalted than the simple major triad. The DO-DI rise produces the illusion of an elevation. This is what makes the stars vibrate, and arouses the feeling of emotional fulfilment. Fig. 110
The difference of 3 key-signatures between E major and C# major denotes the same modal tension that has been called ’axis tension’ in the music of Bartók and Kodály. (Chords based on identical axes – for example C, A, Eb, F# – show a difference of 3, or 3+3=6, accidentals.) The famous ’light chord’ in Haydn’s Creation oratorio blazes up with the same DO-DI rise! The meaning of Eb major
is DO-MI-SO,
what is more, Haydn doubles the effect, by another 3-sharp elevation swinging over from C major to A major. The question suggests itself: what happens in the case of a descent of 3-flat key-signatures? For example, when C major is exchanged by Eb major. Fig. 111
In this case DO major is transformed into MA major (C major into Eb major). The character of the Eb major chord is determined by the MA degree — the melody itself expresses the MI-MA decline (E-Eb theme-opening). Thus the cited melody became the leitmotif of ’dream and sleep’ in Wagner’s Valkyrie. (In b. 3 a similar change is enacted.) The difference of 3 accidentals between C major and Eb major expresses once more an ’axis tension’. The state of deep sleep (daze caused by poison) in Mozart’s Così fan tutte, is symbolized also by MA major tonality: Bb major following the G major key: Fig. 112
Or let us take a MINOR triad, for example, an E minor chord, and replace it by the key lying 3 signatures lower – that is, by G minor. If we consider E minor as a LA-DO-MI chord, the G minor will have a DO-MA-SO meaning, and its character will be determined by the sombre-sounding MA degree. Fig. 113
The recapitulation of the Dies irae in Verdi’s Requiem makes a cruel impression because the dominant B7 leads — not into the expected E minor — but into G minor: DO-MA-SO chords!
Verdi’s most ethereal musical formula is produced by replacing the expected A minor tonic by F# minor: FI-LA-DI (Fig. 115). Its airy and sublimated effect arises from the upward-luring FI and DI degrees. The music reaches, as it were, a point beyond earthly gravitation. Fig. 115
If a triad (either major or minor) is placed a minor-third degree lower, the DO rises to DI — and the sound becomes ’brighter’. When the transposition is carried out in the opposite direction, the tone ’darkens’, because the MI sinks to MA (e.g. in the case of a C major — Eb major change, or A minor — C minor change, the E note is modified to Eb). The DO-DI change implies a rise of 3 sharps, the MI-MA change a descent of 3 flats. An organic part of the cheerful atmosphere in the 2. episode from Kodály’s Dances of Marosszék is that the theme, recurring four times (bs. 108, 120, 132, 144), moves by minor-third steps downwards (that is, in each case it rises by 3 key-signatures) — so that, in passing around the whole C#(Db)–Bb–G–E axis, it becomes brighter and brighter. As opposed to this, the dark and disquieting effect of sequences moving upwards on a minor-third ladder, was already well-known to the Romantic masters. The call-to-death tone at the beginning of the Tristan Prelude would certainly dissolve without this minor-third rise (4-4 bar sequence). In the "Liebestod" theme this process is only accelerated: the melody moves upwards through minor-third degrees – so that, in passing around the whole Ab-B-D-F axis, it becomes darker and darker. Fig. 116
The direct opposition of the two kinds of sequence is particularly effective — as it happens in Bartók’s Violin Concerto: in this way does the first obtain a ’joyful‘, the other a ’struggling’ character: Fig. 117
The refrain-melody of Dances of Marosszék acquires a fervently passionate or a triumphant character according to which colouring element gains the upper hand: the triad a minor third higher (on the first appearance of the theme), or a minor third lower (on the last appearance of the theme): Fig. 118
Tristan’s desire motif — in the course
of the Prelude — emerges in three basic forms:
and thus exhausts the complete F-D-B-Ab axis. Fig. 119
The exposition involves an elevation of 3 key-signatures, the recapitulation implies a descent of 3 key-signatures – while in the middle part, there is no change in tension (a difference of plus 6 = minus 6 signatures is established between F major and B major and, as a result, the two cancel out each other’s opposite tension). In Beethoven’s Missa Solemnis a breath of fresh air flows over the orchestra when in the Gloria movement authentic (V-I) steps alternate with LA-DI-MI effects (B–Ab, Db–Bb, Eb–C, F–D major chords): Fig. 120
In Grigory’s dream-narration from Mussorgsky’s Boris Godunov the text itself indicates this ascension: ’Long flights of stairs led me to the top of a high tower’. The vision is evoked through harmonic sequences deepening by minor thirds: Fig. 121
Casting our net a little wider now, we note that (related to the DO-MI-SO and LA-DO-MI triads), the DI suggests a ’major’ character,
In my previous investigations (between
1947-1974) I worked out almost twenty theoretical deductions of the axis
system. Nevertheless, I have so far overlooked a possibility: namely that
relative solmization could be the most simple means of ’making visible’
the attractions functioning within the system.
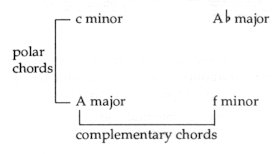
On an elementary level, then, two key-words govern Romantic harmony: DI and MA. However, the most characteristic axis tension is realized in polarity, in the relation of the farthest keys: in the distance of 3+3, that is, 6 key-signatures (e.g. in the connection of A major and Eb major – or A major and C minor). It follows from the above that a polar tension-character can be brought about by modifying DO to DI and, simultaneously, MI to MA. Let us take the simplest relation: C major and its relative A minor. If we replace MI by MA in the C major chord, and DO by DI in the A minor chord, the result will be a DO-MA-SO and a LA-DI-MI triad. Fig. 122
The difference between the 3 flats of C minor and the 3 sharps of A major is 6 accidentals. (A chord based on LA calls to mind a minor triad — whereas a chord based on DO suggests a major triad. In Figs 122-123, however, it is LA major and DO minor that appears!) Tristan’s death motif is, in fact, a materialization
of this polar idea:
The formal turning-point of Isolde’s Liebestod ("wundervoll und leise") reflects a similar opposition: C# minor and A# major. Fig. 124
In Bach’s St. John Passion, the contrast between the soldiers and the Virgin Mary is depicted by D minor and B major harmonies: dark DO-MA-SO and bright LA-DI-MI chords. As B major appears, the scene is suffused by an almost celestial light: ’and at the cross of Jesus stood his mother...’ Fig. 125
At the moment of Otello’s suicide, this order is reversed: the LA-DI-MI comes first, then, with a sudden fall of six key-signatures, the DO-MA-SO chord (D major and F minor). Fig. 126
But let us return to the relative C major and A minor keys, and modify DO to DI and MI to MA! The chord thus created condenses the A7 and Eb7chords polarly (tritonic relationship). Fig. 127
Our next example is the appearance of Parsifal in the flower-garden scene. The basic tonality is represented by C major and the relative A minor (C-E-G and A-C-E). – If we replace DO by DI and MI by MA, the continuation of the theme: the A-Eb-G-C# polar formula will then automatically spring from the C-C# (DO-DI) and E-Eb (MI-MA) steps, Fig. 128
again combining A7 (A-C#-G) with Eb7 (Eb-G-C#=Db). NB: A and Eb mark the ’extreme’ points of the fifth-circle, see diagram of the axis system. This polar character is demonstrated with an almost sensuous force by Fig. 129. At the beginning of Act III, Desdemona and Otello greet each other: Desdemona is still unsuspecting — but Otello is already tormented by the thorn of jealousy. In keeping with this, Desdemona stays harmoniously within the sphere of the tonic E major — C# minor, while the same melody suffers a polar distortion by Otello: he deforms the DO to DI and the MI to MA (E-E# and G#-G turn). Fig. 129
Without precedents of this sort it would be hard to understand how the combined use of DO-DI and MI-MA became regular in Bartók’s music — as we can see for instance in the "Marcia" theme of the Sixth String Quartet. Fig. 130
And finally, we must mention the ’reciprocal’ case of the polar DI+MA tension. Let us take a D major and an F7 chord as an example. The meeting of the two results in a polar effect – as the DO-MI (D-F#) notes of the first chord become DI-MA (D#=Eb and F) notes in the second. Fig. 131
A reverse effect can be created when the two chords are interchanged: in this case the chord bearing polar tension is followed by a sudden resolution. In the Insurrection scene of Verdi’s Don Carlos, the distorted situation is solved by an F7-D major turn: the forbidding figure of the Grand Inquisitor towers above the crowd and with a single gesture forces the rebels to their knees. The effect speaks for itself. Fig. 132
Systematizing what has been said above, we can distinguish essentially three kinds of major, and three kinds of minor triads. Shifting the MAJOR triad by a minor-third interval, the DO changes into DI, or the MI into MA — according to whether we move downwards or upwards. In this manner three kinds of major character come into being: the three types are to be distinguished from each other by the solmizating symbols DO-MI-SO, LA-DI-MI and MA-SO-TA, respectively. Fig. 133
If the operation is performed with MINOR triads, three kinds of minor character will be obtained which can be differentiated by the symbols LA-DO-MI, FI-LA-DI and DO-MA-SO. Fig. 134
That the problem in question is not a theoretical, but a ’live’ one is well exemplified by Verdi’s Falstaff (Act II, scene 2) where A major = DO - MI - SO,
Liszt’s Rákóczy March (Rhapsody XV) is an ’embodiment’ of Fig. 134: the melody itself has an A minor signification (=LA-DO-MI) – accompanied by F# minor (FI-LA-DI) and C minor (DO-MA-SO): Fig. 136
It may seem paradoxical but late Romanticism
discovered a new kind of harmonies: the ’minor’ key (LA key) that has a
major third (DI) – and inversely: the ’major’ key (DO) key that has a minor
third (MA).
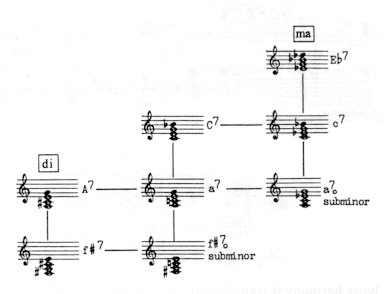
The axis system developed from the classical major–minor tonality in two ways: from the correspondences between relative and parallel major–minor chords. In the simplest case, the parallel mode of C major is C minor – and its relative key A minor. This combination carries within itself the germ of a significant chord-type which became a true emblem of Romantic music (suffice it to recall the well-known ’Tristan chord’ — see Fig. 149 on p. 81): Fig. 137
Since this chord proves to be the ’relative’ of the minor harmony, we call it the subminor chord. In the Parsifal-motif this relative connection takes shape as follows:
To make a distinction between the three basic types, in our harmonic diagrams we shall indicate seventh chords with a major character by capital letters; seventh chords with a minor character by small letters; and seventh chords founded on a diminished triad by a circle under figure 7 (its seventh-note being a minor-seventh interval). Fig. 139
In the example above, between C major and C subminor a ’polar’ tension is established because C major and Eb minor — the latter inherent in C subminor — show a difference of 6 accidentals (similarly to keys facing each other in the circle of fifths). This is why Bartók and Kodály preferred the use of the G subminor – rather than the conventional dominant seventh G-B-D-F:
In the refrain-melody of Isolde’s monologue (Act III), the polar tension of D major and D subminor manifests itself! Fig. 141
* From a dynamic point of view, in the movement
of the major, minor and subminor chords the simplest relationship is created
by the relative key connections, i.e. by a change
(for example, from C major to A minor, from A minor to F# subminor, or from C major directly to F# subminor) — and vice versa.
A change in the direction of the minor or subminor involves an increase in tension, Fig. 143
whereas a change in the opposite direction results in a lessening of tension.
But it is worth mentioning that the change in the relative minor direction is what we discern as a ’natural’ connection, while the change in the other direction creates in a certain sense an ’unnatural’, violent effect. Thus did the melody of Fig. 142 become a ’curse’ motif, and the harmonic motion of Fig. 144 the symbol of the ’dead’ swan. In Liszt’s oratorio Via Crucis the death of Jesus (Consummatum est – XII. station) produces a paralyzing effect because F# minor is followed by the relative A major. Fig. 145
A ’modal’ change is considerably more powerful than a relative change, that is
for example, from C major to C minor, from C minor to C subminor, or from C major immediately to C subminor) – and vice versa. Fig. 146
It should be noted this time, too, that the parallel subminor-minor-major change is what we fell to be ’natural’ (it virtually passes unnoticed if we close Bach’s minor fugues with a major triad). The C# major episode in Kodály’s Dances of Marosszék owes its serene nature-atmosphere precisely to these ’natural’, positive connections, i.e. from major always to the relative minor, and
The harmonies pass through the entire axis-circle in this way: Fig. 147
And conversely, the parallel major-minor-subminor change creates a passionate, short-tempered, dramatic impression! In the middle-part of Liszt’s "R.Wagner, Venezia" (from b. 31) we hear only pure triads, and yet, these triads receive a tragic character since they move in the ’negative’ ’unnatural’ direction, i.e. from minor always to the relative major, and
Fig. 148
It is just as one expect: Isolde’s "Liebestod"
follows the same harmonic thread (see Fig. 188 on p.
99).
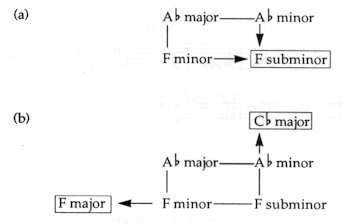
In vain do we challenge classical theory: what is it in the Tristan chord that ’cuts to the heart’ of the listener? Instead of theoretical considerations, we must follow our healthy musical intuition. We instinctively know about the F minor triad that it represents the relative key of Ab major, that is, if Ab major
= DO-MI-SO, then
creating the most fundamental musical relationship. And if we unexpectedly exchange the MI note with the painful dark-coloured MA note, we at once perceive the tension that almost disrupts the chord.
The MA change is well demonstrated by the Tristan-quotation of the Mastersingers.
The ’basic’ form of the Tristan-motif, its typical occurrence is that which starts with an Ab note (as at the end of the Prelude). And if Wagner starts the work with an A note after all, then the polar tension created by the DI+MA notes also becomes tangible. Fig. 151
The subminor may function as a tonic, too. Fig. 150 makes clear that the Tristan-chord: F subminor appears as the relative key of the tonic Ab minor – quasi as a deceptive cadence! The ’F major’ character of the initial step in the overture (A-F) and the B major end of the opera reflects a ’counterpole’ relationship. On the other hand, the final chord of the opera: B major represents the relative major of the ’basic key’ (= Ab minor) and, as such, it suggests a ’death’ symbolism. Perhaps nothing shows the axis-tension of the Tristan chord better than its resolution, which can be performed — according to the axis system — in four different ways, in four directions: towards E, or Bb, or Db, or G. Fig. 152
In Parsifal, too, the love symbol is represented by F subminor, i.e. the Tristan-chord. The emotional ’metamorphosis’ comes about when a Db root gets below the tense Tristan-chord, and this Db — as if by magic — changes the meaning of the F subminor at once: the F-Ab-Cb-Eb notes are transformed into overtones (major third, fifth, seventh, ninth) and, as a consequence, start ’floating’ sensually: Fig. 153
This is how a tense harmony is transformed into ’colour’. The Db bass functions like an acoustic ’prism’ which changes the sense, the colour, the atmosphere of the Tristan-chord. Since we perceive the former basic notes as overtones, their effect will be incorporeal and disembodied. What these and similar solutions may have meant to Kodály is revealed by the following Psalmus-quotation. At the moment subsequent to the dramatic dénouement (’From you he removes your every burden’) the Tristan-chord melts similarly into the Db ninth-chord: Fig. 154
With the aid of relative solmization, the tonal relations can be further simplified. We place the relative connections one beneath the other (e.g. C major, A minor, F# subminor) – and the modal connections side by side (e.g. A major, A minor, A subminor). Fig. 155
The columns of A major, C major Eb major are separated by a difference of 3 accidentals from each other. The ’air pressure-difference’ thus created is also expressed by the fact that the character of the left column is determined by degree DI, and that of the right column by degree MA (C# and Eb notes, respectively). Only one more link is required — either vertically or horizontally — to bring the axis to a close. These ’ascending, descending and collateral’ relations are valid for the other two functions: the dominant and subdominant, too. We will turn again to Verdi, quoting the Ave Maria of Otello: Fig. 156
We note that the upper organ point (Eb) remains common to every chord — which is why we meet tonic and dominant chords only, the former marked below the line, the latter above it. The dominant chords are easily dealt with, three variants appearing altogether (the V. degree: Eb major and Eb minor, and the relative of Eb major: C minor). Of the tonic chords, likewise the parallel connection (Ab major–Ab minor) and the relative connection (Ab major–F minor) prove to be the most direct. These three chords provide the conditions for the F subminor as well (see Fig. 157 a). The F minor and Ab minor harmonies, however, are to be connected not only ’inwards’ (by means of F subminor) – but also ’outwards’, in the direction of F major and Cb major: the parallel of F minor being F major, and the relative key of Ab minor being Cbmajor:
F major and Cb major not only polarize the sound (they are counterpoles), but also create a homogeneous tonal unit: Fig. 158
The continuation of Fig. 138 on p. 77 (Parsifal theme) rests on the F# major– C major pendular movement. Fig. 159
The 12 bell-strokes from the night-scene of Verdi’s Falstaff serves as a model example for the subdominant. (As the F note of the bell remains unchanged in each chord, only tonic and subdominant harmonies are to be found.) All the permutation are exhausted by Verdi.
* As stated before in the axis system it is not degrees IV and V that most potently represent the subdominant and dominant functions – but the degrees which divide the circle of fifths into three equal parts. The wide emotional range of the love-duet of Otello and Desdemona is attributable to the fact that the ’depth’ of the subdominant and the ’height’ of the dominant are strained to the utmost (Fig. 161). As compared to the tonic Gb major, the negative tension of the subdominant can be enhanced if the IV degree Cb major (B major) is replaced by its upper minor third degree: D major. — On the other hand, if the positive tension of the dominant is to be enhanced, we must put in the place of the dominant V degree (Db major) its lower minor-third degree: Bb major. In this way, the tonic Gb, the D subdominant, and the Bb dominant come into an augmented triad relation. Fig. 161
At the end of Act III, the augmented triad cadence C-Ab-E almost bursts the framework of tonality.
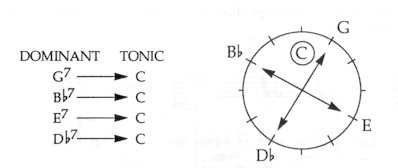
* It appears from the diagram of the axis system that — in the case of C tonality — a dominant–tonic cadence may assume the following forms: Fig. 163
(1)
The fourth step upwards corresponds to the classical V—I cadence (G7®
C).
Theoretically, these four forms can readily be traced back to the structure of the axis system. Nevertheless, the clue to the individual character of each form of resolution again lies in the modal quality of the theme. Let us begin with the ’modal’ dominant: Bb7 ® C After the dominant Bb major seventh we would expect an Eb major tonic – and if (instead of Eb) C major surprisingly emerges, this means that the place of the expected DO basic note (Eb) has been occupied by DI (note E)! In this way, the tonic has also become sharpened and more elevated. Fig. 164
Bartók’s Violin Concerto is introduced by a pendulum of tonic (=B major) and modal dominant (A7) chords. Fig. 165
In Act I of Otello, the Jago–Roderigo duet becomes more and more tense due to the use of modal dominants. Fig. 166
Thus in each subsequent chord, instead of DO, DI comes; this is in perfect harmony with the text, which speaks of ranks (of the difference between the envied captaincy and the subaltern rank of ensign); it is as though Jago were standing on tiptoe, the words "mio!" are amplified by the DI degrees. By the way, perhaps these Romantic models help us better understand why Bartók and Kodály preferred the use of the modal dominant to the dominant fifth-degree (in which the influence of folk-music naturally played a considerable role). The inverse procedure of the modal dominant is the III. degree dominant (major- third step downwards): E7 ® C the dominant seventh chord is succeeded not by the usual A major (DO-MI-SO) — but by C major: MA major chord. Fig. 167
At the deepest point of Otello (Fig. 162 on p. 87), the end of Act III, the impact of the E major—C major close is the more shocking since the place of the expected MI degree is taken by MA (C note). This is the reason why the III-I cadence is so heavily laden with death-symbolism. In Il Trovatore it appears when Leonore admits she is ready to die: III. degree G major followed by Eb major tonic: Fig. 168
Isolde’s death in Wagner’s Tristan is accompanied by a whole chain of III-I cadences. The keys follow one another in axis order. Fig. 169
Let me refer to the Gloria of Beethoven’s Missa Solemnis. The heroic F major dominant in "Qui sedes ad dexteram patris" is followed by a MA major tonic (Db), which is why the "Miserere nobis" causes anxiety and disquietude (F ® Db = III-I cadence). In Verdi’s Requiem, a III-I cadence casts a shadow of doom upon the recapitulation of the "Dies Irae" theme: after the B major dominant a G tonic emerges — hence the shock effect (see Fig. 114 on p. 69)! The III-I cadence may also figure as an onomatopoeic ’colouring’ element. At the start of the second scene – in Act II – Mistress Quickly attempts to imitate: to parody Falstaff’s deep, full-throated voice. The change of tone occurs through a III-I cadence: E7 ® C (see Fig. 135 on p. 76). * In short, the modal dominant–tonic cadence has a positive meaning, while the III-I cadence gives a negative impression. From the above it follows that a contrary effect can be attained if the same key has been prepared for by the lower major second degree (modal dominant), or the upper major third degree (III). Two Bb major themes from the Masked Ball suggest themselves here – the first introduced by an Ab major, the other by a D major dominant. Renato’s first aria is the manifestation of a friend’s love and devotion. But the very same Bb major key, following right after the dramatic turn: at the exposure of Amelia (in the second act) has an infernal impact, expressing scathing sarcasm. Fig. 170
If the dominant and tonic chords are exchanged, their meaning will also be reversed! In the case of the I-III turn:
the E7 will be related to the A major key – which lies 3 sharps higher than C major. Thus the III. degree will produce the effect of ascent (a ’light’ effect – chiaro). On the other hand, in the case of the modal dominant following upon the tonic I. degree,
the Bb7 will be related to the Eb major key –which lies 3 flats lower than C major. The modal dominant will thus produce the effect of descent (a ’shadow’ effect – oscuro). Here are some examples for both. The lofty effect of the Aida theme may be attributed to the fact that the tonic is succeeded by a III. degree dominant.
In contrast to this, the dramatic turning point in Rigoletto: the blast of "La sua figlia!" is evoked by a modal dominant, subsequent to the tonic (F tonic and then Eb dominant). Fig. 172
For Beethoven, the major-third change became the means for expressing ’mystic absorption’ (III-I) or ’transubstantiation’ (I-III):
To sum up, the
meaning. These regularities may also be extended
over the relationship of the subdominant and tonic (or dominant and subdominant)
functions. We may consider it a general rule that
effect. We still owe the intepretation of the Phrygian dominant (minor-second step downwards), for example
In the Phrygian dominant — just as in the classical V. degree seventh — the ’leading’ role is played by the sensitive notes TI and FA: the leading note TI pulls towards the root (DO), and the FA towards the MI. Fig. 174
The sensitive notes TI and FA halve the octave; therefore they are interchangeable — without any change in their relationship. Thus TI and FA are common notes in both the V. degree dominant and in the Phrygian dominant; as we see from the example above, the third and seventh note of the G7 is identical with the seventh note and third of the Db7 dominant. In the Recruiting Music of Háry János, Kodály exchanges the dominant seventh (G7) with its counterpole (Db7) — and in this way, the Phrygian dominant is reached. Fig. 175
We quote a typical Bartók example, too: this resolution is reserved by Bartók for a sudden ’change of scene’:
An interesting combination of the Phrygian dominant and V. degree dominant can be observed in Wagner’s Mastersingers, at the appearance of the night-watchman.*) Fig. 177
* It is easy to survey these interrelationships – if we realize that from the DOMINANT G seventh chord four different TONIC degrees can be reached:
We quote the final scene: ’ecstasy of immortal love’ (”l’estasi d’un immortale amor”) from Verdi’s Aida. Ab major stands for the V. degree dominant in bs. 3-4, D major for the Phrygian dominant (b. 7), and F major for the III. degree dominant (b. 8). In the middle of b. 4, also the modal dominant emerges for a moment: B minor (!). The glorification (’I see the heaven opening’, bs. 5-6) is associated with a LA-DI-MI rise: Bb major. Fig. 178
In his late style, Verdi accords a singularly large scope to the diminished seventh chords. These diminished seventh chords, however, turn out to be not real diminished sevenths - but such major seventh harmonies (chords of DO-MI-SO-TA pattern) whose DO root ’overstrains’ to DI. A classical example of this DI-change is the "Barrabam!" exclamation in Bach’s St. Matthew Passion: instead of the tonic D major, the threatening D#-F#-A-C diminished seventh emerges. Fig. 179
The diminished seventh C-Eb-F#-A accompanying Desdemona’s murder begins as a modification of the B seventh chord (B-D#-F#-A) and ends polarly: in an F seventh chord (C-Eb-F-A). Fig. 180
Authentic cadences occur at every step in Verdi’s music, like this:
It is, however, a well-tested practice to replace one or another of the major seventh chords by diminished sevenths. In our example (the stretta from the opening scene of Falstaff), almost every chord is replaced by a diminished seventh - without veiling or overshadowing the S-D-T-S-D-T (subdominant-dominant-tonic) meaning of the sequence. Fig. 181
The diminished seventh belongs to the family of distance chords: it divides the tonal system into four equal parts. Hence it follows that any diminished seventh can supplant four different major-seventh harmonies. In the storm scene of Otello, Verdi exhausts all combinational possibilities: Fig. 182
Through the chromatic lowering of any note of the diminished seventh chord a major seventh can be achieved (e.g. from the C#-E-G-Bb diminished seventh the C-E-G-Bb major seventh). If the next third is also lowered, we shall obtain a minor seventh (C-Eb-G-Bb) - and lowering the subsequent third, a subminor chord emerges (C-Eb-Gb-Bb). Reversing the process, the harmonies start widening systematically (subminor-minor-major-?). Verdi takes advantage of this possibility in the tonal construction of the "Credo". In our tonal system three different diminished
seventh chords ( (1)
a ’tonic’: by raising the root of the C seventh chord, a C#-E-G-Bb
(Every other form agrees with one or other
of the above formulae.) As we see, the ’tonic’ diminished seventh contains
a DI and TA note. However, the root of the major and minor keys is represented
by DO and LA, respectively.
The harmonies of ’Grand Romanticism’ frequently obtain some sort of ’background’ meaning - a secondary, transposed sense - and this occurs whenever a major triad is replaced by the minor chord lying a major-third higher (e.g. C major substituted by the E minor chord). Or, on the contrary, when a minor triad is replaced by the major chord lying a major-third lower (e.g. A minor substituted by the F major chord),
that is: the DO-MI-SO major triad is substituted by MI-SO-TI - or the LA-DO-MI minor triad by FA-LA-DO. For example, in the Rigoletto-Gilda duet, the substitute chord (E minor replacing C major) reflects Gilda’s spiritual purity: the substitute chord invests the melody with a ’sublime’ emotional content. Fig. 184
As opposed to this, the tragic weight
and baleful atmosphere of Kodály’s Psalmus Hungaricus lies
in that the melody of A minor origin is inserted into an F major harmony
- right at the beginning of the work. (See: Fig.
67 on p. 40)
Distinction must be made between a FA-MI and a MI-FA step, as is suggested by the opening of the hymn Ode to Joy in Beethoven’s Choral Symphony. The spiritual transparency of the song originates in the MI-FA initial notes.**) On the one hand, MI-SO-TI became the ’transcendental’ unearthly element of late Romanticism. On the other hand, the FA-LA-DO lends the music some sort of emotional ’depth’ or weight. From the notes of the C major (or A minor) scale, six perfect triads can be formed: besides C major and A minor, the 1-sharp G major and E minor - as well as the 1-flat F major and D minor (cf. L. Bárdos: Modal Harmony). Therefore
are identical with the ’positive’ and ’negative’ substitute chords, respectively. The ’major’ substitute chord (F major) intensifies the ’minor’ character of the theme, while the ’minor’ substitute chord (E minor) intensifies the ’major’ character of the melody. In the former, the F-C perfect fifth reinforces the minor third (DO) of the root (A) - while in the latter, the E-B perfect fifth reinforces the major third (MI) of the root (C). It is enough to glance at Fig. 183 to see that the two kinds of substitution (MI-SO-TI and FA-LA-DO) are again each other’s reflections - precise mirror images - in comparison to RE. Now we can complement our previous observations (pp. 78-81): the change from major to the minor substitute chord is perceived as a ’positive’: elated turn (e.g. from C major to E minor) - and conversely, the change from minor to the major substitute chord produces a ’negative’ downward-pulling effect (from A minor to F major, for example). But at the same time, the negative substitute chord makes a ’natural’ impression - while the ’positive’ substitute chord creates an ’unnatural’ effect. From these facts it emerges that negative or positive effects may also be piled up! It pertains to the dolorous atmosphere of the Parsifal theme quoted in Fig. 42 on p. 30 that two negative effects - parallel major-minor and substitute minor-major turns - alternate with each other: C minor, Ab major, Ab minor, Fb (=E) major, E minor, C major, C minor. If we reverse this sequence, then parallel minor-major triads alternate with positive (=minor) substitute chords. The theme thus created is well-known to us from Tristan (NB: it stems from the opening cello-motif of the opera: A-F-E-Eb-D): Fig. 185
Let us think back to the beginning of Parsifal; where C minor substitutes for the tonic Ab major. The ’elevated’, immaterial tone of the melody emerges from here:
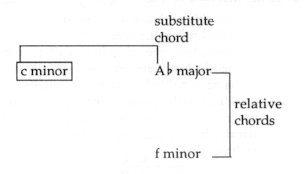
In the ’death motif’ of Tristan, however, the tonic C minor was overshadowed by the heavy Ab major (see: Fig. 123 on p. 73). Let us remain within the sphere of Ab major and C minor: the substitute chord of Abmajor
is C minor,
In other words, if we treat the Ab major as a DO-MI-SO chord, the meaning of C minor will be MI-SO-TI. On the other hand, if we consider C minor as a LA-DO-MI chord, the meaning of Ab major will be FA-LA-DO. Combining Ab major with C minor a symmetrical chord - the so-called ’hypermajor’ harmony is produced (see: pp. 40-41). Its construction is: major triad with a major seventh - Ab-C-Eb-G. It adds considerably to the peculiar quality of these chords that the positive substitute chord falls within the range of the dominant, while the negative substitute chord falls within the range of the subdominant. Fig. 186 (in Ab major) receives a dominant tinge through the positive C minor - while Fig. 123 (its tonic being C minor) assumes a subdominant shade through the negative Ab major opening chord. From Fig. 183 it emerges that the relationship of C major and E minor is determined by the C-B step,
i.e., by the melodic turns: Fig. 187
In a minor key, the deceptive cadence (VI. degree chord appearing instead of the tonic I. degree) may play the role of the substitute chord - especially if it loses touch with the tonic I. degree and becomes independent. The key to Isolde’s "Liebestod" also lies here: in b. 3 the Cb major deceptive cadence emerges as the negative substitute chord of Eb minor!
The duet of Rigoletto and Gilda "Piangi, piangi, fanciulla piangi" brims over with sorrow by appearing not in the expected F minor, but in Db major - after the dominant C (Db = substitute chord and, at the same time, a deceptive cadence - which loses touch with the tonic F minor). In the minor key, the I. degree relates to the deceptive cadence (degree VI) - as degree IV relates to the Neapolitan chord. Thus, in the minor key there exists an analogy between the Neapolitan chord and the deceptive cadence. In East European folk music the ’leading notes’ FA-MI and TA-LA play a determining role, calling forth a ’plagal’ (subdominant-tonic) relationship and, at the same time, a substitute relationship (F major-A minor and Bb major-D minor). If we invert the above chords - around the RE symmetry center - an ’authentic’ (dominant-tonic) cadence is produced by means of the TI-DO and FI-SO ’leading note’ steps:
In Wagner’s "Opus Metaphisicum" (as Thomas Mann called the Tristan), these chords suggest a high aspiration - an abstract "Gothic" passion - like in Scene 3 of Act I, in the opening three bars: Fig. 190
Under certain conditions, negative substitute chords may suggest a specifically Eastern, whereas positive substitute chords a specifically Western way of thinking. (a) It is a rule in melodies with a six-four character and MI-LA-DO structure that the ’tension-chord’ (the dissonant ’changing chord’ of the tonic) is represented by FA-LA-DO - and this comes about when the MI root is raised to the FA degree (through a Phrygian step!). Fig. 191
The ominous atmosphere of Desdemona’s leitmotif in Act IV is determined by the G#-C#-E six-four chord - its dissonant ’changing chord’ being A-C#-E (=a negative substitute chord): Fig. 192
(b) As stated above (Fig. 186 on p. 98), MI-SO-TI is the transfigured, unearthly element of late Romanticism. In Verdi’s Requiem the beginning of the work (in A minor) is laden with oppressive death-symbolism. But the very same A minor theme at the recapitulation receives a transcendental character - since it reappears as the ’positive’ substitute chord of F major: now it makes visual the perpetual light. Fig. 193
Remarks on Verdi’s colour chord Let me refer to the modification of the cadential I six-four chord. In almost every significant major-theme of Otello, the I. degree six-four chord is coloured by its substitute chord; the E major cadence, for instance, by the G# minor harmony. At the end of the ’kiss-theme’, a D# note appears instead of the usual tonic E.
Verdi exchanges the SO-DO-MI six-four chord for the positive SO-TI-MI substitute chord: we hear a TI note - in place of the accustomed DO (or, at least, a SO-TI-MI chord colours the dominant). This relationship is even more unequivocal in the motto theme of Falstaff: ’We’ll cuckold him - neatly!’ (A minor-F major cadence). Fig. 195
In Verdi’s music this most complex (and perhaps most beautiful) ’colour chord’ (Fig. 194 above) is composed of a major triad, and two additional elements: the seventh note (A) ranging below the fundamental note, and the major sixth (G#) ranging above it. Between these two notes a major seventh relationship is established (A-G#). Historically, Verdi’s colour chord developed from the ’dominant’ chord. It is interesting to note that also Debussy favoured this type, for example in La Mer (we quote Movement III, No 44): the ’acoustic’ scale of the melody appears above a B-D#-A seventh chord (A=seventh note) - the top-note of the theme is G# (=major sixth of the root): Fig. 196
We grasp the importance of this colour chord if we call in mind occurrences like the ’diatonic’ form of the fugue-theme in Bartók’s Music for Strings, Percussion and Celesta (Movement IV, b. 204). The C ’acoustic’ scale is accompanied by two organ points: the major sixth above the root (A) and the seventh note below the root (Bb): Fig. 197
* The most powerful contrast is created by the complementary keys (See: pp. 31-33). After a dominant seventh (G7) we expect a C major or a C minor tonic. C major can be substituted by E minor, and C minor by Abmajor. The ’command’ motif in Tristan ("Befehlen liess") is introduced by a dominant G7 and followed by the E minor and Ab major substitute chords - in place of C major or minor. The E minor and Ab major triads, as we know, merge in a 1:3 model. Fig. 198
The opening theme of Bartók’s Fourth Quartet is a true ’challenge’ to the aesthetes. Fig. 199
Bars 1-2 and 3-4 constitute a question-and-answer relationship. Therefore the end of b. 2 corresponds to the traditional dominant half-close cadence. (We note that in bs. 1-2 the viola part is silent and thus a contrast - a ’split’ - is produced between the violins and the cello.) At the end of b. 2, the last chord is a B minor triad in the cello (= the substitute chord of the dominant G major), and an Eb major triad in the violins (= the substitute chord of the dominant G minor). - As a result, the two substitute chords unite in a 1:3 model. The "Klang" character is determined by the fact that in this instance the 1:3 model consists of two separate augmented triads. Fig. 200
The same combination (Eb major + B minor) occurs in Movement II of the ’Dance Suite’ - at the appearance of the Ritornello! In addition, the theme itself (taking on a modal character) is conceived in G.
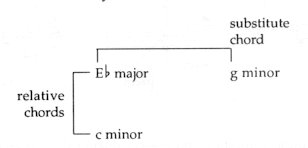
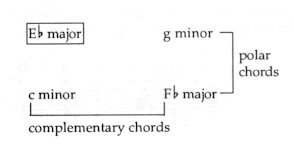
In Romantic music, the individual harmonies appear not as ’atoms’ but as elements of a ’giant molecule’ (a compound arrangement of tones resulting in an organic structure and unity) - where all particles are associated and closely interlinked; and as a consequence, every chord has an organic connection with every chord. Starting from a major melody, e.g. from Eb major, the substitute chord of the tonic is G minor - and its relative key is C minor: Fig. 202
The question arises: which is the chord that could establish a contact between these two triads (i.e. G minor and C minor)? The ’complementary’ key of C minor is Fb major - while the polar key of G minor is likewise Fb major (= a difference of 6 key-signatures): Fig. 203
The melody quoted from Verdi’s Aida consists of the four chords outlined above. Even the closing cadence - at the end of b. 4 - contains a G minor chord (and in addition, the polar Fb-Ab-D seventh chord also blends into the Bb dominant seventh). Fig. 204
Let us choose now a minor theme - e.g. C minor. In this case, the substitute chord is Ab major (= a negative substitute chord), and the relative key of Ab major is F minor: Fig. 205
This time, the connecting link between F minor and C minor is created by A major - because the A major triad constitutes the complementary chord of F minor and the polar chord of C minor (= a difference of 6 key-signatures): Fig. 206
On p. 73 we quoted the Death-motif from Wagner’s Tristan (Fig. 123). The basic tonality is C minor. The structure of the theme is determined by the chords described above. In our first example the positive substitute chord, in our second example the negative substitute chord prevails; what is more, both examples start with the substitute chord of the tonic. In the Verdi example we find tonic and dominant, whereas in the Wagner example tonic and subdominant chords only. As a matter of course, this duality predestines the content, the character, the colour and even the ’lifestyle’ of the two melodies. Judging from the analysis of Romantic
music, one might speak of the surprising frequency - one might even say
preponderance - of substitute chords, which (taking into account the ambiguity
inherent in Romantic harmony) reveals something characteristic of Verdi’s
or Wagner’s ’double spirited’ harmonies.
I am inclined to think that it was two linguistic elements which made possible the development of the dialectic system of Western music: the discovery of the ’tension-resolution’ system of atonality and tonality - and the discovery of polymodal tensions. Bach is credited with sowing the seeds which determined the evolution of music for two subsequent centuries. The very first sentence of St. John Passion can give proof of this. When the ’divine’ element is set against the ’devilish’, what does Bach do but oppose the idea of ’tonality’ to that of ’atonality’: Jesus is represented by the nearest natural overtone, i.e. the perfect fifth, whereas Judas’s symbol is the diminished fifth - an interval expressing the distance principle in the most direct way, because it symmetrically halves the tonal system (as well as the diminished seventh, which quarters the fifth-circle). Fig. 207
The characteristic ’tension-resolution’ system of Western music could scarcely have evolved without the antagonism of the tonal and the distance principles; moreover, this opposition - an age-old struggle between tonal asymmetrical and
elements - became a seminal impulse in the development of European music. The characteristic ’tension’ chord of Baroque music Fig. 208
is represented precisely by that diminished seventh harmony which divides symmetrically the fifth-circle round the RE symmetry center (and RE-SI symmetry axis) of our diatonic system. (See. Fig. 214, first diagram on p. 110). Every key has accordingly a ’tonal’ center and a ’symmetry’ center (e.g. in the E major key, the tonal centre is E - while the symmetry-axis of the E major scale is F# or C). However, the idea of consonance and dissonance is only one structural element of this tonal world. The other element is that tension-principle which is made possible by polymodal thinking. In St. John Passion, at the very first words of Jesus, we feel as though the very air has changed since Bach renders the miracle tangible by replacing the F major harmony with the 3 sharps higher D major: the same elevation arises here that caused the sound to ’brighten’ in our first Verdi example (Fig. 109 on p. 67). Fig. 209
* To give a summary, the main idea of Otello: the ’kiss-theme’ includes in a concentrated way everything that has been said above.
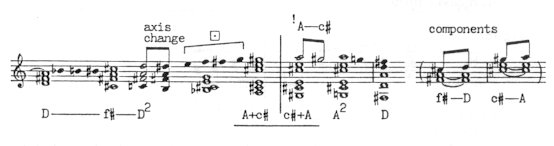
It emerges literally from the ’sea’: the C#-E-G-A# tones. The modal structure of the theme would serve as a model example. In order to step from E major into the relative C# minor, or the relative A# subminor, we have to move the fifth of E major - the note SO - to LA or FI (the note B to C# or A#). The opening bar of the kiss-theme is almost an embodiment of this principle. Fig. 211
The real driving force of the melody, however, lies in the polymodal changes - namely in the potential differences between E major-E minor and C# major-C# minor-C# subminor. Fig. 212
From b. 4 on (Fig. 210),
the major and minor characters alternate periodically: the MI and MA in
the bass change from bar to bar.
These two substitute chords (G# minor and C major) constitute a 1:3 model - and, as such, annihilate each other’s tonality due to the atonal character of the 1:3 model. The symbol of Otello’s excitement: the DI rise (E#) also plays a constructive role in the theme: middle of the melody (b. 4)! Note the contrast between the FI (A#) in b. 2 and the FA (A) in b. 3. The FI-FA change is one of the most peculiar phenomena in Romantic harmony - of which more see: pp. 144-145.***) The middle of b. 4 contains a LA-DI-MI (C# major) triad, while b. 5 involves a DO-MA-SO (E minor) triad: a difference of 6 key signatures has been reached. It has been frequently observed in Verdi or Wagner that the ’fulfilment’ is realized in the major sixth of the tonic (we have termed it the ’pastoral’ sixth); this is accomplished in the culminating sixth bar of the kiss-theme, too! Madách’s psychology applies to the gloomy ’C major’ following the fulfilment: ’The price of the kiss’s honey is in the dejection which comes after it’. NB: the MI-RE-DO motif rounding off the theme which (after the inserted C major) continues the pentatonic scale of b. 6, is the symbol of repose and smoothing throughout the work. The pentatonic scale in question (Fig. 213) creates a counterpole relationship with the pentatonic opening chord of the work (cf. Fig. 93 on p. 54): Fig. 213
Thus, the beginning and end of the opera
reflect a pole-counterpole relation.
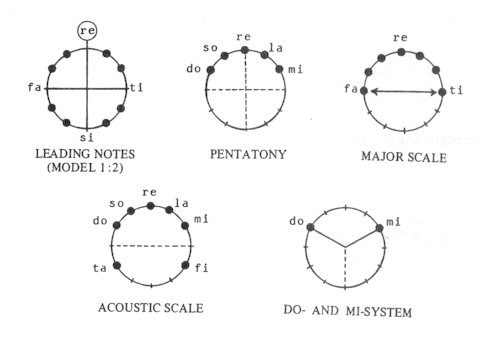
We have established: asymmetry is coupled with tonal, symmetry with atonal relations. The symmetry-center of our tonal system is constituted by the RE. If we divide the fifth-circle symmetrically around the RE central note - by way of halving - we will obtain RE-SI and FA-TI tritones (see the first sketch below). - It is not by chance that the role of the dissonant ’sensitive notes’ is filled by the tritone TI-FA in the major key, and by the tritone SI-RE in the minor key. This is how the LEADING NOTES came into existence. PENTATONY in this system is represented by the five upper notes (second sketch in the Figure). From the 5-note system we arrive at the 7-note system by expanding pentatony by one degree upwards and one downwards: the extreme points (FA and TI) thus enter into a tritonic relationship with each other (third sketch), originating the ’tensest’ points of the scale. Therefore, the major scale (compared to the RE-center) fills in the upper arc of the circle of fifths. The missing notes result in pentatony. Thus the pentatonic and seven-note scales mutually complement each other. The ACOUSTIC scale (harmony) became a static ’colour’ chord because it lacks the two sensitive notes that characterize the major key: TI and FA (fourth sketch in the Figure). NB: in this sense, the major scale can be considered a ’tensional’ scale. If we omit the ’atonal’ degrees of our first sketch from the 12-degree system, model 1:2 is created: the basic scale of chromaticism (DO-DI-MA-MI-FI-SO-LA-TA eight-note scale). The two most static points of our tonal system: DO and MI coincide with the ’asymmetry’ points of the system (fifth sketch in the Figure). DO and MI reflect a major third relationship.
Let us summarize the fundamental phenomena of polymodal chromaticism (this is how Bartók himself called his own style) - on the basis of the position the 12 degrees occupy in the system. If we group the 12 notes of the chromatic scale into symmetrical pairs (in relation to the RE center-note), the meaning of the individual degrees will be as follows:
The four polymodal colouring elements - DI, MA, FI, TA - enable the following combinational possibilities. Jointly, MA+FI produce a passionate (=MA), but at the same time, an elevated (=FI) atmosphere. On the other hand, TA+DI embody a specifically Hungarian (oriental) attitude (TA = bent for ’melancholy’, and DI = bent for temper and impulsiveness). The DI+FI together create a cheerful, even transcendental character. The MA+TA, however, bring about a sorrowful or languid character. Finally, the DI+MA bring about a polar tension (’choleric’ temperament) - while FI+TA represents balance: see acoustic (overtone) harmony. This study has attempted at defining the place of ’relative solmization’ in musicology. As far as I am concerned, I believe this method to be the missing link which might connect abstract theoretical research with living music. According to Eddington, the theoretical mathematician working with symbols of his own creation never knows what he is doing. It is the duty of the practical physicist to recognize that playing around with letters might reflect or describe such structure systems that could yield him knowledge about the existing physical world: armed with the abstract plan of structure he penetrates external reality once deemed unfathomable - the function and nature of which would, with traditional means, be beyond his grasp and comprehension. With the seemingly primitive symbols of relative solmization, I have attempted to draw the map of a musical world that manifests itself elementarily in these symbols - provided we know what the operations concern. I consider Kodály’s concept (based on our capacity to identify any pitch in relation to a tonal center) to be a clue which enables us to pull down that boundary which separates theory from everyday experience and leads us directly to the structure and contents of music; and at the same time, it is also suited to the historical analysis of the musical material.
*) Concerning the reversed turn - minor second upwards - see Fig. 188 on p. 99 (ed.) **) Concerning FA-MI step, see p. 144 (ed.) ***) The fourth polymodal alteration (TA) is also present (D - b.4) (ed.)
|