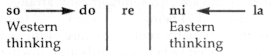The most characteristic feature of Bartók and Kodály’s technique is the dual treatment of material. 

In my analytical studies, I have used the terms ’pentatonic’ and ’acoustic’ (system) to describe the two aspects of their music.

Systematically, the two basic types are mirror images of each other. If, in the most general way, we have defined the ’chromatic—pentatonic’ technique as obeing the rules of the Fibonacci series, then the diatonic overtone system is none other than the exact counterpart — systematic inversion — of the chromatic rules.

Pentatony has its source in Eastern folk music; accordingly it is of melodic origin. The overtone (acoustic) system, on the other hand, is rooted in Western traditional music and is therefore of harmonic origin.

The overtone system is controlled by the laws of physical consonance. (Harmony is perfect when the closest overtones are merged in it.) In the major triad our ears register the most simple arithmetical proportions. A major chord represents an order based on the simultaneous sounding of notes – thus it is vertical in construction: it has a ’spatial’ extension.

Pentatony, on the other hand, is of melodic origin. And since melody presupposes tones following each other in ’time’, it has a horizontal, linear extension.

The primary distinguishing mark of pentatonic cultures is the descending DO-LA minor third and LA-MI fourth (as a cadence). The derivation of DO-LA and LA-MI cannot be traced back to the laws of physical consonance. Just the opposite. Pentatony reflects a peculiar tension (which could well be termed ’life tension’) and is justified by the organic – physiological – disposition of our ears. This implies that while the overtone system suggests arithmetical proportions, the pentatonic system owes its tension-character to the most simple geometric progression – which governs organic development of ’natural’ growth.
 

DO system and MI system 

In Western musical cultures the feeling of tonality is created by the triad conson-ance: the ’con’-sonanceof the third and fifth. It was the prelude and folk choruses of Mussorgsky’s Boris Godunov that first made me feel that there exists a musical culture radically different from European harmonic thinking. The archaic quality of these melodies resides in their six-four structure.

Fig. 77

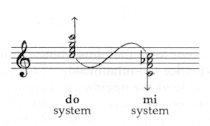
In the Hungarian folk song below the keynote and tonal resting point is the C. Both the harmonic and the tonal meanings of the quoted melody are determined by the ’MI pentatonic’ structure. This harmony is not F minor – but it is a scale based on C as a root:

Fig. 78

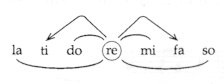
And this six-four harmony (C-F-A^b) is not the second inversion of the root-position F minor triad; consequently, it is not a secondary formation but a musical element equal in rank with the root-position triads.

A distinctive feature of melodies on MI as keynote is that the root is frequently reinforced with a ’leading-note’ step: the Phrygian FA ® MI turn (Fig. above). – NB: the Phrygian scale is a MI scale!

The basic step of the plagal ’six-four’ system is the LA ® MI cadence, while the basic step of classical harmony is the authentic V–I dominant–tonic SO ® DO cadence. Perhaps nothing demonstrates better the relationship of Western and Eastern ways of thinking than the fact that (in relation to the RE symmetry center) the authentic SO ® DO cadence of classical music and the plagal LA ® MI cadence, are precise mirror images of each other:

the DO and its reflection, the MI, can alike serve as the tonic fundamental note:

Fig. 79

The overtone system follows the law of free-fall (delineated in the fifth-circle, it points towards thesinking direction) while the pentatonic system obeys the principle of tension and, as such, acts against the law of free-fall.

If the dominant-tonic cadence, characteristic of Western music, is represented by the G⁷ ® C chords, then we can take it for granted that the ’mirror image’ of this formula (related to the RE symmetry center)gains an Oriental colouration. This cadence is well-known to us from the Prelude of Act III of Tristan. The sensitive notes TI and FA play an important role in both instances. But while in the V-I cadence theTI-DO leading note step comes to the fore, the oriental colouration originates from the FA-MI ’leading note’ step. 

Fig. 80 

As in classical harmony, the TI ® DO leading-note step affirms the tonic DO keynote, so in this style of expression, the FA ® MI step reinforces the MI tonal keynote. Not to mention that, in relation to the REsymmetry center, the TI ® DO and FA ® MI leading-note steps occupy a symmetrical position – and they move symmetrically as well:

The notes of the acoustic scale are also symmetrically arranged – around the RE symmetry-axis (the mirror-image of FI being TA). (See: Fig. 214 on p. 110)

Degree RE constitutes the symmetry center not only of the pentatonic scale, but of the major and minor scales as well (where upwards and downwards from the RE, each interval has its exact mirror image):

The relative major and minor keys therefore show an inverted relation to each other – as compared to the RE. (See the relationship of C major and A minor in Fig. 183 on p. 96). The unison melody at the opening of Wagner’s Tristan — the Sailor’s Song — appears in two basic forms: one accompanied by a SO pedal point – and the other by a MI pedal point. In the former it is the SO-DO, in the latter it is the LA-MI that determines the tonal quality of the song – thus the first takes on a ’major’ and the second a ’minor’ character.

Fig. 81

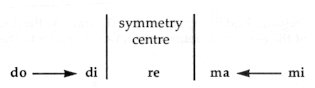
Let us bring also degrees DI and MA into the above relation – creating a polar tension. The symmetrical position of the DO ® DI and MI ® MA steps — in comparison to RE — is again evident:

The basic scale of Bartók’s chromaticism is, as we know, the 1:2 model. If we add degrees DI+MA to the notes of the above example, model 1:2 is created:

Fig. 82

While DI and MA appear as expressive ’tensional’ elements, FI and TA appear as impressionistic ’colour’ elements, the former taking on a dynamic, the latter a static character.
 

The complementary relation of the two systems

The harmonies of the chromatic and diatonic systems are ’Janus-faced’ harmonies. They form contrast in unity. The two harmonic spheres complement each other to such an extent that the 12-note scale can be separated into a ’golden section’ sequence and an acoustic sequence (D^b— Phrygian step! — and B, as chromatic degrees, require a chromatic interpretation).

Fig. 83

The characteristic intervals of the two harmonic worlds complement each other like the positive and thenegative of a photograph:
 
 

In the Háry Prelude, Kodály opposes the MI scale to the DO scale: the C=MI-pentatonic theme of theexposition returns with DO character in the recapitulation:

Fig. 84

Inverted relation of the two systems

But the relationship between the two systems is multidimensional. The elements of the pentatonic and acoustic systems not only complement but also reflect each other: through the inversion of the 8, 5, 3, 2 steps, acoustic intervals are produced, and vice-versa:
 
 

In Bartók’s Cantata Profana, too, D represents the tonal key-note. The beginning scale and closing scaleof the work are each other’s mirror images – note for note.

Fig. 85

The opening of the work rises out of MI pentatony (D-F-G-B^b-C framework) — while the framework of the closing theme is DO pentatony (D-E-F^#-A-B) — and both scales are coloured by degrees FI and TA. The closing scale will therefore take the shape of an ’acoustic’ scale (DO-RE-MI-FI-SO-LA-TA-DO), whereas in the opening theme we find a diminished fifth — TA — instead of a perfect fifth.

In his Harvard Lectures Bartók himself made reference to the MI scale in question.^*

The basic tonal idea of Bartók’s Cantata Profana had already been realized by Liszt in his Via Crucis – its form built on the ’reflecting’ relationship of the DO and MI systems. The beginning and end of the work are alike rooted in the D keynote. But while the former develops from MI pentatony (D-F-G-B^b theme of six-four character) – the latter shows its exact inversion, thus closing the work with a DO scale.

Fig. 86

Bartók’s Sonata for Two Pianos and Percussion reflects a similar structure: the principal theme ofMovement I fills out the MI pentatonic frame: C-E^b-F-A^b, while the principal theme of the final movement gains a firm DO character (C major chord!) – being at the same time a perfect acoustic (overtone) scale.

Fig. 87

In Bartók’s and Verdi’s music alike, the direct confrontation of the two systems form the ’mainmasts’ ofthe work. In Bartók’s Sonata for Two Pianos and Percussion, the dramatic metamorphosis takes place on the border-line of Movements II and III. The end of the second movement is a six-four chord based on C (C-F-A^b), the beginning of the third movement, however, is founded on a C major chord – with an acoustic scale.

In Beethoven’s Missa Solemnis, "sepultus est" is associated with a six-four chord based on C (C-F-A^b-C), whereas "et ascendit" with a C major harmony (cf. Fig. 79 on p. 45).
 
 

Consonance and dissonance

It follows from the very nature of the acoustic system that its formations are consonant: owing to theovertone relations only consonant intervals take place in it; whereas elements of the Fibonacci system are precisely those regarded as dissonant by classical theory.

In the acoustic system the most powerful dissonance is embodied in the Fibonacci intervals 2, 3, 5, 8 (thatis: minor subdominant harmonies). Within the pentatonic system, however, this is also inversely true! In melodies based on the 3, 5, 8 structure, the most vigorous dissonance coincides with the appearance of the perfect fifth.

The opening theme of Kodály’s Háry János (Fig. 84 a on p. 48) rests upon the C=MI pentatonic scale (C-E^b-F-A^b-B^b) in which the perfect fifth marks the point of highest tension (TI degree!) and this C-G dissonance calls for a resolution (as in classical harmony, the fifth-dissonance is also to be treated heavily: the accentuated G note occurs in a strong metrical position).

We give a typical folksong example, too:

Fig. 88

Openness and closedness

The most direct experience (the most profound at the same time) is the duality existing between the ’closed’ world of chromaticism and the ’open’ sphere of the acoustic system. The closed Fibonacci-models produce a tense and dynamic effect; the open overtone harmonies create a balanced and static impression. Also the melodic lines follow this principle: in the closed world of the chromatic system, the themes are most naturally joined with circular, rotary motions – whereas in the open diatony, with straight scale-lines (see Fig. 105 on p. 63).

It evolves from the dynamic nature of the chromatic system that its formations are in a continuous progress of expansion or contraction – hence the frequency of ’scissor’ themes, ’funnel’ motifs, canons in ever-widening distances, ’fanshaped’ progressions, and so on. In the diatonic technique, however, there is no trace of these pulsating progressions; acoustic harmonies are characterized by stability and constancy.

The duality of openness and closedness is also expressed in the number relations. The acoustic system rests on whole numbers (multiplying the fundamental tones vibration by 2, 3, 4, 5, 6, 7, 8, etc., we obtain an overtone scale). On the other hand, the key-number of the pentatonic system is irrational – just like the p of the circle (about the role of the geometric mean in Bartók’s music, see chapter Nature Symbolism). Also the 3:5:8 proportion is only roughly accurate.

Finally, let us raise the question: how can we pass over from the plagal six-four system to the authenticmajor-minor system? There are two possibilities.

     (a) By means of a tonal answer, we can change the E-A-C six-four chord into the A-C-E root-position triad. The unison principal theme of Psalmus Hungaricus is a model of this procedure:

Fig. 89

NB., in the middle of the melody (bs. 5-6) the antitonic C-G-D, and the modal dominant G major emerge: within the theme these represent the ’tension function’.

     (b) But the change is even more effective if the six-four chord based on E (E-A-C or E-A-C^#) is resolved by the triad of the same name: i.e. E major or E minor. In fact, a similar change happens to the melody of the Bartók's Second Quartet, too, at the very end of the first movement:

Fig. 90

The question here is why DO and MI are the most static points of the two tonal systems. As we know, tonality can be established only through the asymmetrical division of the tonal system. If the tones of pentatony are arranged in a fifth-order (see: Fig. 214 on p. 110), the most perfect asymmetry is realized in the outer degrees: in DO and in MI. The individuality of DO pentatony is decided by the fact that it can be exclusively built up of perfect fifths. The character of DO pentatony is therefore the most ’materialistic’. On the other hand, that of MI pentatony is the most incorporeal and disembodied, as not a single perfect fifth can be built on the MI root. Consequently, the DO scale is ’material’, while the MI scale is ’spiritual’ (abstract) in character, suggesting an ’inner’ world.

This dualism was already realized by Wagner. The Parsifal-bells ’sound differently’ in the first and in the third act. The four-note motif C-G-A-E gains a ’C’ meaning in the former and an ’E’ meaning in the latter:

Fig. 91

This difference in character was already recognized by Verdi in Otello.The inaccessible figure ofDesdemona is painted with MI-centered pentatony, whereas Jago’s down-to-earth materialism is depicted with DO-based pentatony. It is remarkable that the notes of the two scales are identical.

Fig. 92

On the other hand, degree RE — as symmetry center — proves to be the most unstable point in the scale: symbolically speaking, within the pentatonic scale the RE represents the point of ’atonality’, which is why it has such a floating effect. One single pentatonic harmony (the opening chord of the opera!) is enough for Verdi to set the ’storm music’ of Otello whirling. The secret of the effect is that the chord is founded on RE; the RE-character is further emphasized by the LA-DO-MI-SO meaning of the G-B^b-D-F notes:

Fig. 93

In our 12-degree system (and this is well shown by the external look of white and black keys on our keyboard instruments, or by our system of notation), — besides degree RE — there is to be found one more symmetry center – and this is the tritone of RE: the ’SI’ degree (in case of C tonality, the G^#=A^b note).

Thus chromatic and diatonic systems are phenomena which have developed not unrelated to each other but they represent the two sides — negative and positive aspects — of the same musical cosmos. They affirm and deny, exclude and at the same time presuppose each other. They form contrast in unity.

Duality and synthesis^*)

I would like to attempt here an intepretation of Bartók’s dual world, his ’yang-yin’ technique, in terms ofan equation, contrasting some special elements encountered at every step in Bartók’s compositions. This interpretation is particularly applicable to the construction and content of the Sonata for Two Pianos and Percussion.
 
 

The principle of duality meant the possibility of synthesis for Bartók. He was not only aware that F^# and C were counterpoles but also knew what it meant to get from darkness into light; he does not only teach us to see dialectic opposites in chromaticism and diatony but also shows the way from Inferno to Paradiso.