We study chocolate games that are variants of a game of Nim. In this
article you can cut the chocolate in 3 directions, and we represent the
chocolates with coordinates
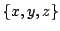
, where
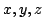
are the maximum times you can cut it in each direction.
The coordinates
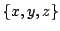
satisfy the inequality
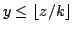
for a fixed natural number
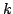
.
For
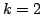
the authors discovered a formula for loser' s states of the chocolate. For
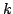
=1 the authors made predictions for the formulas for loser' s states, although they have not managed to prove them.
They also present some interesting graphs made by the set of L states of the chocolate games for
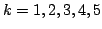
.