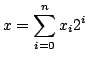 ,
,
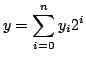 and
and
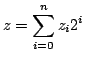 with
with
In this section we prove Theorem 1.2, and
we need several facts about the relations between numbers in base ![]() , the nim-sum of numbers and the floor function.
, the nim-sum of numbers and the floor function.
| (2.5) |
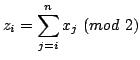 and
and
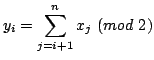 for
for
| (2.8) |
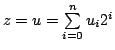 . By
. By 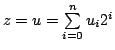 . By
. By | (2.14) |
| and |
(2.15) |
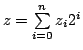 and
and
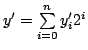 . Clearly
. Clearly
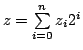 and
and
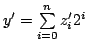 . Then we have
. Then we have
By Lemma 2.4
For ![]() there exists
there exists
![]() that satisfies one of the following two conditions
that satisfies one of the following two conditions ![]() and
and ![]() .
.
![]()
![]() satisfies
satisfies
![]() and
and
![]() , then by
the fact that
, then by
the fact that
![]() for
for
![]() we have
we have
![]() for
for
![]() , and hence by the fact that
, and hence by the fact that
![]() we have
we have ![]() . Therefore we have
. Therefore we have ![]()
![]() Let
Let
![]() , then
, then
![]() and
and
![]() . By the fact that
. By the fact that
![]() for
for
![]() we have
we have
![]() for
for
![]() , and hence by the fact that
, and hence by the fact that
![]() we have
we have ![]() . Let
. Let
![]() , then we have
, then we have ![]() .
.
Next we are going to define the function
![]() for a state
for a state
![]() of chocolates.
of chocolates.
![]() is the set of all states that can be reached from the state
is the set of all states that can be reached from the state
![]() in one step (directly).
in one step (directly).
Next we prove that if you start with an element of ![]() , then any move leads to an element of
, then any move leads to an element of ![]() .
.
| (2.16) |
| (2.17) |
Next we prove that if you start with an element of ![]() , then there is a proper move that leads to an element of
, then there is a proper move that leads to an element of ![]() .
.
By Theorem 2.3 and 2.4 we finish the proof of Theorem 1.2. If we start the game with a state
![]() , then by Theorem 2.3 any option by us leads to a state
, then by Theorem 2.3 any option by us leads to a state ![]() in
in ![]() . From this state
. From this state ![]() by Theorem 2.4 our opponent can choose a proper option that leads to a state in
by Theorem 2.4 our opponent can choose a proper option that leads to a state in ![]() . Note that any option reduces some of the numbers in the coordinates. In this way our opponent can always reach a state in
. Note that any option reduces some of the numbers in the coordinates. In this way our opponent can always reach a state in ![]() , and finally he wins by reaching
, and finally he wins by reaching
![]() . Therefore
. Therefore ![]() is the set of L states.
is the set of L states.
If we start the game with a state
![]() , then by Theorem 2.4 we can choose a proper option leads to a state
, then by Theorem 2.4 we can choose a proper option leads to a state ![]() in
in ![]() . From
. From ![]() any option by our opponent leads to a state in
any option by our opponent leads to a state in ![]() . In this way we win the game by reaching
. In this way we win the game by reaching
![]() . Therefore
. Therefore ![]() is the set of W states.
is the set of W states.