3. Chocolates without simple formulas for L-state

In this section we study the chocolate of Fig 3.1. The mathematical structure of this chocolate is interesting when it is compared to that of chocolate of Definition 1.4. While the chocolate of Definition 1.4 has a simple formula for L states, this chocolate has complicated formulas for L states.

Figure 3.1  

We define a new type of chocolate precisely. Please compare this to the chocolate in Fig 3.1, since an example of this definition is the chocolate of Fig 3.1.

Definition 3.1   We make a triangle $OAB$ on the 2 dimensional plane with two coordinates by connecting three points $O(0,0)$ ,$A(ns,nt)$ ,$B(2ns,0)$ with segments, where $s,t > 0$ and $n$ is a natural number.
We connect points $(is,it)$ and $(2is,0)$ with segments for $i = 1,2,...,n-1$ , and we also connect points $(is,it)$ and $((2n-i)s,it)$ with segments for $i = m+1,m+2,...,n-1$ . We make a trapezoid with four points $(ms,mt)$ , $((m+1)s,(m+1)t)$ , $(2(m+1)s,0)$ ,$(2ms,0)$ , and color this trapezoid with red. We color all the other parts of the triangle $OAB$ with green. All the segments are in black.
green polygons are sweet chocolate that can be eaten, and the red trapezoid is the bitter chocolate that cannot be eaten.

Figure 3.2  

You can cut these chocolate along the segments in three ways.
$(1)$ You cut parallel to the segment $AB$ on the left side of the red trapezoid.
$(2)$ You cut horizontally above the red (bitter) trapezoid.
$(3)$ You cut parallel to the segment $AB$ on the right side of the red trapezoid.
Therefore it is proper to represent these chocolates with $\{x, y, z\}$ , where x,y,z stand for the maximum numbers of times that we can cut these chocolate in each direction. For example in Fig 3.1 we can cut 2 times at most parallel to the segment $AB$ on the left side of the red trapezoid, 5 times at most horizontally and 5 times at most parallel to the segment $AB$ on the right side of the red trapezoid. Therefore $x=2$ , $5 = 2$ and $z=5$ . Therefore we represent the chocolate in Fig 3.1 with the coordinates $\{2,5,5\}$ .

Although we do not have a simple formula for the set of L states in the case of this chocolate game, we have some prediction for the set of L states.
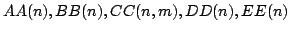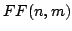First we define six functions $AA(n),BB(n),CC(n,m),DD(n),EE(n)$ and $FF(n,m)$ for natural numbers $n,m$ .

Definition 3.2   $AA(n) = \{ \{6 n - 1,4 n - 4 k - 1, 4 n + 2 k - 1 \},k= 0,1,..., n - 1\} \cup ... ...k= 0,1,..., n - 1\}\cup \{\{6 n - 1, 4 k + 1, 6 n + 2 k\}, k= 0,1,..., n - 1\$

$BB(n) = \{\{6 n, 4 n - 4 k, 4 n + 2 k\}, k= 0,1,..., n\}\cup \{\{6 n, 4 n - ... ... k= 0,1,..., n - 1\}\cup \{\{6 n, 4 k + 3, 6 n + 2 k + 2\}, k= 0,1,...,n - 1\}$

$CC(n,m) = \{\{6 n + 1, 4 n - 4 k - 1, 4 n + 2 k + 1\},k= 0,1,..., n - 1\}\cu... ...1,..., n - 1\}\cup \{\{6 n + 1, k + 4 n + 1, k + 8 n + 2\},k= 0,1,..., n + m\}$

$DD(n) = \{\{6 n + 2, 4 n - 4 k + 1, 4 n + 2 k + 1\},k= 0,1,..., n\}\cup \{\... ...,1,..., n - 1\}\cup \{\{6 n + 2, 4 k + 3, 6 n + 2 k + 4\}, k= 0,1,..., n - 1\}$

$EE(n) = \{\{6 n + 3, 4 n + 2 - 4 k, 4 n + 2 k + 2\},k= 0,1,..., n\}\cup \{\... ... 3\},k= 0,1,..., n\}\cup \{\{6 n + 3, 4 k + 1, 6 n + 2 k + 4\},k= 0,1,..., n\}$

$FF(n,m) = \{\{6 n + 4, 4 n - 4 k + 1, 4 n + 2 k + 3\},k= 0,1,..., n\}\cup \... ...,1,...,n - 1\}\cup \{\{6 n + 4, k + 4 n + 3, k + 8 n + 6\}, k= 0,1,...,n + m\}$

By using Definition 3.2 we present a prediction for the set of L states.

Prediction 3.1   $\cup_{m,n\in Z_{\geq0}}(AA(n) \cup BB(n)\cup CC(n,m)\cup DD(n) \cup EE(n) \cup FF(n,m))$ is the set of L-states of the chocolate game of Fig $\ref{defofchoconoformula}$ .

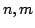There is another prediction for the set of L states.

Prediction 3.2   $\{\{\lceil{(3a)/2}\rceil +2n,a,a+2n\};a,n \in Z_{\geq0}\}$ $\cup \{\{3n+1,a,a+1+2n\};a,n \in Z_{\geq0}$    and $n \leq \lfloor {a/2} \rfloor \}$ $\cup \{ \{2n+\lfloor {a/2}\rfloor+1,a,a+1+2n\};a,n \in Z_{\geq0}$    and  $n > \lfloor {a/2} \rfloor \}$ is the set of L-states of the chocolate game of Fig $\ref{defofchoconoformula}$ .

Remark 3.1   The authors do not present proofs of Prediction 3.1 and Prediction 3.2. Prediction 3.2 looks quite simple, but to prove it is difficult. In fact one of the authors have proved Prediction 3.2, but the proof was 40 pages long. Therefore the authors looked for another formulas for L states, and discovered Prediction 3.1. This prediction looks complicated, but the authors think that the proof of this prediction will not be lengthy.
Instead of proving these prediction, the authors present the calculation by computer algebra system Mathematica.
By calculation of Mathematica these predictions seem to be true.

Example 3.1   This is a Mathematica program to calculate L states of the chocolate games of Definition 3.1. By variable 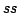$ss$ we determine the size of the data.

ppo[ss_] := Block[{k}, k = 1;
  al = Flatten[Table[{a, b, c}, {a, 0, ss}, {b, 0, ss}, {c, 0, ss}], 
    2];
  allcases = Select[al, (1/k) (#[[3]]) >= #[[2]] &];
  move[z_] := Block[{p}, p = z;
    Union[Table[{t1, p[[2]], p[[3]]}, {t1, 0, p[[1]] - 1}],
     Table[{p[[1]], t2, p[[3]]}, {t2, 0, p[[2]] - 1}],
     Table[{p[[1]], Min[Floor[t3/k], p[[2]]], t3}, {t3, 0, p[[3]] - 1}]
     ]
    ];
  Mex[L_] := Min[Complement[Range[0, Length[L]], L]];
  Gr[pos_] := Gr[pos] = Mex[Map[Gr, move[pos]]];
  pposition[0] = Select[allcases, Gr[#] == 0 &]]

Example 3.2   This is a Mathematica program to calculate the set in Prediction 3.1.

AA[n_] := 
  Union[Join[
    Table[{6 n - 1, 4 n - 4 k - 1, 4 n + 2 k - 1}, {k, 0, n - 1}], 
    Table[{6 n - 1, 4 n - 4 k - 2, 4 n + 2 k}, {k, 0, n - 1}], 
    Table[{6 n - 1, 4 k, 6 n + 2 k - 1}, {k, 0, n - 1}], 
    Table[{6 n - 1, 4 k + 1, 6 n + 2 k}, {k, 0, n - 1}]]];
BB[n_] := 
  Union[Join[Table[{6 n, 4 n - 4 k, 4 n + 2 k}, {k, 0, n}], 
    Table[{6 n, 4 n - 4 k - 3, 4 n + 2 k + 1}, {k, 0, n - 1}], 
    Table[{6 n, 4 k + 2, 6 n + 2 k + 1}, {k, 0, n - 1}], 
    Table[{6 n, 4 k + 3, 6 n + 2 k + 2}, {k, 0, n - 1}]]];
CC[n_,m_] := 
  Union[Join[
    Table[{6 n + 1, 4 n - 4 k - 1, 4 n + 2 k + 1}, {k, 0, n - 1}], 
    Table[{6 n + 1, 4 n - 4 k - 2, 4 n + 2 k + 2}, {k, 0, n - 1}], 
    Table[{6 n + 1, 4 k, 6 n + 2 k + 1}, {k, 0, n}], 
    Table[{6 n + 1, 4 k + 1, 6 n + 2 k + 2}, {k, 0, n - 1}], 
    Table[{6 n + 1, k + 4 n + 1, k + 8 n + 2}, {k, 0, n + m}]]];
DD[n_] := 
  Union[Join[
    Table[{6 n + 2, 4 n - 4 k + 1, 4 n + 2 k + 1}, {k, 0, n}], 
    Table[{6 n + 2, 4 n - 4 k, 4 n + 2 k + 2}, {k, 0, n}], 
    Table[{6 n + 2, 4 k + 2, 6 n + 2 k + 3}, {k, 0, n - 1}], 
    Table[{6 n + 2, 4 k + 3, 6 n + 2 k + 4}, {k, 0, n - 1}]]];
EE[n_] := 
  Union[Join[
    Table[{6 n + 3, 4 n + 2 - 4 k, 4 n + 2 k + 2}, {k, 0, n}], 
    Table[{6 n + 3, 4 n - 4 k - 1, 4 n + 2 k + 3}, {k, 0, n - 1}], 
    Table[{6 n + 3, 4 k, 6 n + 2 k + 3}, {k, 0, n}], 
    Table[{6 n + 3, 4 k + 1, 6 n + 2 k + 4}, {k, 0, n}]]];
FF[n_,m_] := 
  Union[Join[
    Table[{6 n + 4, 4 n - 4 k + 1, 4 n + 2 k + 3}, {k, 0, n}], 
    Table[{6 n + 4, 4 n - 4 k, 4 n + 2 k + 4}, {k, 0, n}], 
    Table[{6 n + 4, 4 k + 2, 6 n + 2 k + 5}, {k, 0, n}], 
    Table[{6 n + 4, 4 k + 3, 6 n + 2 k + 6}, {k, 0, n - 1}], 
    Table[{6 n + 4, k + 4 n + 3, k + 8 n + 6}, {k, 0, n + m}]]];
	na[tt_] := 
  Union[Flatten[
    Table[Join[CC[n, m], FF[n, m]], {n, 0, tt}, {m, 0, tt}], 2], 
   Flatten[Table[Join[AA[n], BB[n], DD[n], EE[n]], {n, 0, tt}], 1]];

Example 3.3   This is a Mathematica program to calculate the set in Prediction 3.2.

dat[nn_] := 
  Join[Flatten[
    Table[{Ceiling[3 a/2] + 2 n, a, a + 2 n}, {a, 0, nn}, {n, 0, nn}],
     1], Flatten[
    Table[If[
      n <= Floor[a/2], {3 n + 1, a, a + 1 + 2 n}, 
	  {2 n + Floor[a/2] + 1, a, a + 1 + 2 n}], {n, 0, nn}, {a, 0,
       nn}], 1]];

Example 3.4   This is a Mathematica program to compare the sets presented in Prediction 3.1 and 3.2. We use Mathematica programs in Example 3.1, Example 3.2 and Example 3.3. By these calculations these predictions seem to be true.

In[1]:= Complement[ppo[8], dat[9]]
Out[1]= {}
In[2]:= Complement[dat[9], na[8]]
Out[2]= {}
In[3]:= Complement[na[8], ppo[90]]
Out[3]= {}
In[4]:= Complement[ppo[90], dat[90]]
Out[4]= {}