Chocolate games that are variants of nim and interesting graphs made by these games.

Shunsuke Nakamura,

Daisuke Minematsu,

Takeru Kitagawa,

Youichiro Naito,

Ryohei Fujii,

Takuto Hieda, and

     Ryohei Miyadera  

Kwansei Gakuin University (Japan)

(runners@kwansei.ac.jp)

Abstract:

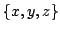
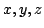
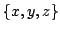
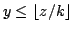
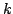
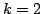
We study chocolate games that are variants of a game of Nim. In this article you can cut the chocolate in 3 directions, and we represent the chocolates with coordinates $\{x, y, z\}$ , where$x,y,z$ are the maximum times you can cut it in each direction. The coordinates $\{x, y, z\}$ satisfy the inequality $y\leq \lfloor z/k \rfloor$ for a fixed natural number $k$ . For $k=2$ the authors discovered a formula for loser' s states of the chocolate.  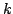For $k$ =1 the authors made predictions for the formulas for loser' s states, although they have not managed to prove them. They also present some interesting graphs made by the sets of L states of the chocolate games for $k = 1,2,3,4,5$ .
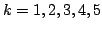
If you are interested in the beauty of mathematics and not in the theory of mathematics, please read Section 4 (Some interesting graphs).