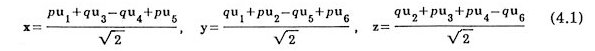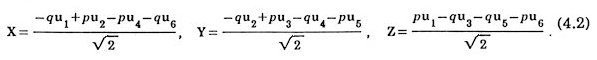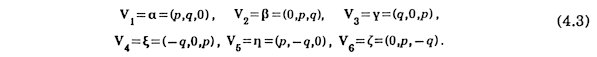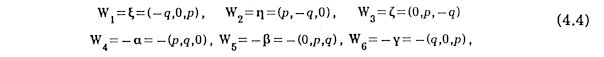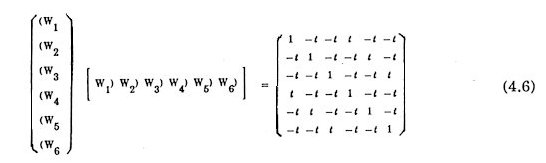|
3. The primitive Projection Method Projection of a regular lattice of higher dimension into the real physical space of lower dimension is a very useful method to construct a model structure of general lattices unifying usual lattices and quasilattices; the well-known examples are one-dimensional quasilattice as a projection from two-dimension, 2D-PT from five-dimension and three-dimensional quasilattice from six-dimension. Calculations with computer are easily carried out by this method. Sometimes they are done without recognizing the features of the structure. It is, at the same time, a merit and demerit of this method. The procedure to construct a d-dimensional general lattices from a D-dimensional simple lattice can be summarized as follows. (1) Regard the D-dimensional original space W as direct sum of d-dimensional physical space W and d (= D - d ³ D/2)-dimensional pseudospace W = W1 Å W2. (2) Select the lattice points in W whose projection to the pseudospace lies in a certain region GC (the gazing crystal) which is defined as a projection of a D-dimensional hypercube. A general lattice G is the projection of them to the physical space. A quasilattice Q is a general lattice without periodicity. Let L be a D-dimensional vector from a lattice point to another lattice point. L= L1Å L2 , Li Î Wi (i= 1 and 2) (3.1) G ={L1; L2 Î GC Ì W2} Î W1 (3.2) (3) Now, the projection from W to W1can be regarded as a mapping from W2 to W1. When the mapping is an injection, the general lattice is a quasicrystal. Therefore, all the informations of an infinite quasiperiodic arrangement in the GC in the whole universe of physical space W1 are concentrated in a small region GC in the pseudospace W2. A whole network is collapsed into the small area GC, keeping its connectivity. Some fortune teller decodes she informations contained in the inside of GC into everything in physical space by gazing it. It is the reason why the area is referred to as the gazing crystal (GC). In the projection from 2-dimension to one-dimension, the point sequence {yn} in GC is very similar to a chaotic behaviour in point sequences in a dynamical mapping or a Poincare mapping of a dynamical process. General cases can be regarded as chaotic motion in multi-dimensional or branching time from this point of view. From a conceptual point of view, the method
is summarized as
and
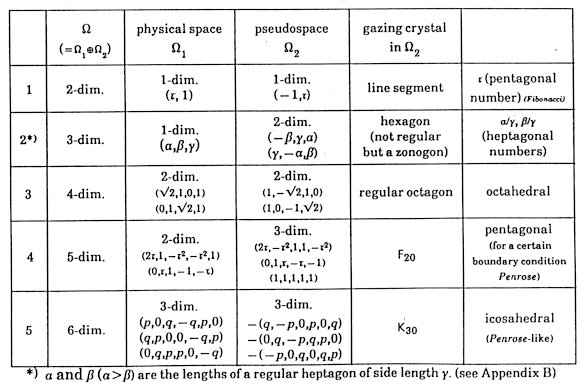
It is noted that a gazing crystal is a compound of DCD-d unit cells because it is a projection of D-dimensional hypercube into (D-d)-dimensional space. It rigorously leads to an important conclusion that there are no simple repeat of any pair of the same unit cells in the primitive projection model. It is the most characteristic feature of the model. Some examples of the gazing crystals are listed in Table 7.
Table 7: Examples of Gazing Crystals
In Example 2, the primitive projection model, being (..LMLSMLMLSMLLMSLMLMSL..) has no self-similarity. There are several transformations leading to a self-similar arrangement. For example, L ® LM, M ® LS, S ® M (LMLSLMMLMLSLSLMLSLMM..) and L ® LMS, M ® LM, S ® L (LMSLMLLMSLMLMSLMSLML..). These sequences can be regarded as either of symbol sequence or point sequence of relative separation lengths L : M : S = a : b : g (in the foot note of Table 7) = a : b : 1 (in Appendix B). In Fig.1, the gazing
crystal of the third example (4-dim. to 2-dim.) is shown. The closer the
point in the gazing crystal, the higher the symmetry or the wider the ruling
area of the local symmetry of the corresponding point in the physical space.
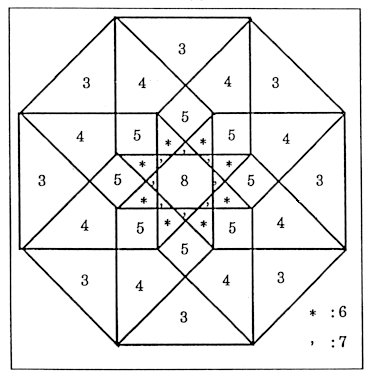
It is noted that the primitive projection method exactly corresponds to
the transformation method in this case. The corresponding Penrose transformation
is shown in Fig.2.
Fig.1 The Gazing Crystal
of Example 3 in Table7.
Fig.2 The corresponding
Penrose Transformation.
Suppose a 6-dimensional simple hypercubic lattice where the lattice vectors are {uk; k = 1,2,...,6}. Introduce another orthonormal set (x, y, z, X, Y, Z) in the sixdimensional original space W so that they are expressed in terms of uk's as.
and
The space is regarded as the direct sum of three-dimensional physical space W1 spanned by (x, y, z) and three-dimensional pseudospace W2 spanned by (X, Y, Z). Six renormalized quasilattice vectors are the renormalized physical-spacecomponents of six bases of the original space. They are
in the Cartesian coordinate system (x, y, z) above. Here a , b, g, x, h and z are given in Eq.(2.1). The arrangement of {±Vk; k = 1,2,...,6} has icosahedral symmetry. The renormalized pseudospace-components of six bases of the original space are three-dimensional vectors.
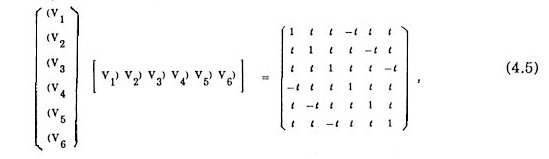
in the Cartesian coordinate system (X, Y, Z) above. The arrangement of twelve {±Wk; k = 1,2,...,6} has icosahedral symmeetry too. The inner products among {Vk; k = 1,2,...,6} and among {Wk; k = 1,2,...,6} are summarized respectively in a matrix form.
and
Being a three-dimensional projection of a six-dimensional hypercubic domain, GC is a rhombic triacontahedron K30 whose edges are either of six unit vectors Wk's (see Chapter 2). Having icosahedral symmetry, K30 is rather spherical. The radii along three kinds of symmetry axes and to the edges are tabulated in Table 8.
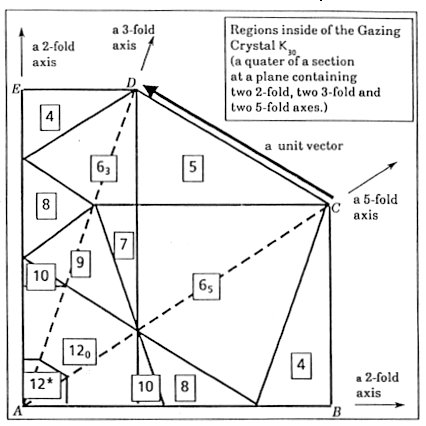
Table 8 Several Radii r of a Kepler 30-hedron K30 of Edge length 1 For a while, a tiling is regarded as a network composed of only unit vectors and its connectivity is mainly investigated. Never mind here that the body-diagonal length of O among extremely short ~0.963. A neighbour in this aspects may be referred to as a vectorial neighbour. The variety of the vectorial environment of a point in physical space is nine types so long as the network structure concerns; the number of vectorial neighbours is either of 4, 5, 6 (two types), 7, 8, 9, 10 or 12. It is convenient to classify the 12-neighbour case into two cases as to be mentioned below. Then there are altogether ten types. These ten local structures as vectorial environment of a point have their associate domains in GC which are respectively denoted by 4, 5, 63, 65, 7, 8, 9, 10, 120 and l2* in Fig.3.
Fig.3 The gazing crystal
K30 for 6-dim, to 3-dim. projection. Only a quater
SELF-SIMILARITY The domain 12* corresponding to the central point of Fl60 is exactly similar of factor t-3 to the whole GC with the centre as the centre ot similarity. Suppose a similar domain of factor t-2. Domain 120 is obtained by removing the domain 12* from it. The points in the domain correspond to the point in physical space with 12 vectorial neighbours but not the centre of Fl60. In other words, not only A6's but some O6's share the point. The similar triacontahedral domain 120 of side length t-2 outside of 12* is for the points with twelve neighbours, which do not correspond to Fl60 but the compound of 2n O6's and (20 -n) A6's (n>0). Let Sl (k)Vl be the summation over five unit vectors among twelve vectors {± Vk; k = 1,2,...,6} whose Vk-component is t = 5-1/2. Then the following relations hold for the mutually associated two vectors in the physical space and the pseudospace
It is a remarkable fact from which a kind
of self-similarity of factor t3 follows. Suppose Q and
Q
+ Wk are both in GC and their associate
points P and P + Vk are both quasilattice
points in the physical space. Let Q*= -t3Q,
regarding
Q as a vector from the centre of GC.
Then Q* lies in the region 12* and Q* + Wk*
= -t3(Q
+ Wk) also lies in 12*. Correspondingly P* and
P*
+ Vk* are both quasilattice points. Both points
Q*
+ Wk and Q* + Wk*
-Wk
lie in domain 65, for any k if Q* lies in 12*.
The vector Sl(k)Wk
corresponds
to the symmetry axis of F20 in physical space. Then the tiling
thus obtained by the primitive projection method has the same skeleton
structure as that by the Penrose transformation mentioned in Chapter
2. Note that the primitive projection method is deterministic and there
are some freedom in the transformation method. This difference is discussed
in the next subsection.
INSIDE OUT AND OUTSIDE IN As mentioned above, the points in 12* sketch a rough structure in physical space in a scale of t3. More detailed structure in physical space is reflected in other region of GC. Generally speaking, a rough structure are reflected in the central parts and the details or their internal structure are in the outer parts of GC. The correspondence between a point in physical
space and a point in pseudospace can be regarded as a mapping, since two
spaces are correlated as the projection of a 6-dimensioiial vectors. A
golden rhombus specified by two V's is mapped into a golden rhombus specified
by the corresponding two W's where the angle of two V's and that of two
W's are supplementary.
A6 « O6 An acute rhombohedron A6 specified by three V's is mapped into an O6 specified by the corresponding three W's where the principal diagonal is multiplied by t-3. An obtuse rhombohedron O6 specified by three V's is mapped into an A6 specified by the corresponding three W's where the principal diagonal is is multiplied by -t3. Though each of rhombohedra is mapped into
a rhombohedron, thus mapped rhombohedra are mutually overlapping in pseudospace.
Then the mapping of a compound of some rhombohedra is complicated. Let
us investigate the mapping of an F20 and K30.
F20 in physical space ® a 30-hedron with bottle neeck in pseudospace (Fig.4(a)) In Fig.4 points are connected so that the whole configuration of these points may be clearly seen than their point to point correspondence. As a connectivity of unit vectors, the points which correspond to the surface points in physical space construct a collapsed rhmbohedral 20-hedron with unit side length. As a three- dimensional point configuration, they are regardes as 22 vertices of a 30-hedron with bottleneck, among whose 30 faces 10 are equilateral triangles, the other 10 are another kind of equilateral triangles and the last 10 are trapezia. A set of four internal points in physical
space is mapped into the outside of the polyhedron ((1)-(4)) in Fig.4(a))
They must be in the gazing crystal. This requirement is rather strong.
Thus the internal configuration of F20 in physical space is
uniquely determined by the position of the polyhedron in tne gazing crystal
in pseudospace.
K20 in physical space ® a concave 60-hedron with icosahedral symmetry in pseudospace (Fig.4(b)) The attitude in drawing Fig.4(b) is the same as in Fig.4(a) except that along and perpendicular to a 3-fold axis instead of a 5-fold axis. The 32 surface points of K30 in physical space are aranged with icosahedral symmetry. Then they are mapped so that the symmetry is kept. However their radii get smaller as given in Table 9.
Table 9 Several Radii of a Concave 60-hedron in Pseudospace 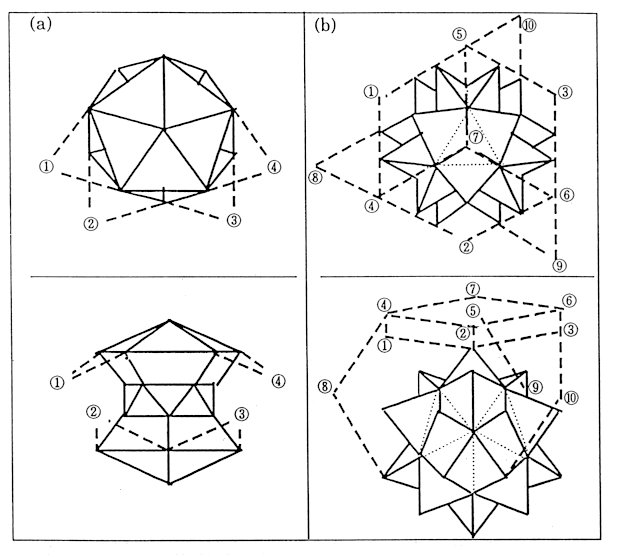
in the physical space. (1)-(4) correspond to the internal points in the physical space. (b) A concave 60-hedron in the pseudospace,which corresponds to F20 in the physical space. (1) - (10) correspond to the internal points in the physical space. The whole distribution of these 32 points
are regarded as a 60-hedron which is constructed by putting a triangular
pyramid on each of 20 faces of an icosahedron whose circumradius is r5.
As for the 10 internal points in physical space, they are mapped to the
outside of the polygon as shown as (1)-(10) in Fig.4(b).
Here an internal configuration with trigonal symmetry is chosen.
C ® an overlapping compound of two concave 60-hedron (Fig.5) C is an overlapping of two K30's where an O6 ((2)-(3)), whose points are all on the surface of eithier of two K60's is shared in common. Among the points of two A6's (1)-(2) and (3)-(4), those but (1), (2), (3), and (4) are internal of either of the K30's. In the case of the maximum symmetry shown in Fig.5, the diameter of the sphere that contains all the mapped point is the maximum. In this case, some of the mapped points are inevitably on the edge of the gazing crystal. Though all of the points (1)-(10) are outside of both 60-hedra ((1)-(3) and (2)-(4)) in the case of the maximum symmetry, the following should be noted. Points (2), (5), (6) and (7) are the internal of K30 ((2)-(4)) but not of K30 ((2)-(4)). Points (3), (8), (9) and (10) are outside of K30 ((2)-(4)) but not of K30 ((1)-(3)). Therefore in less symmetrical cases, two O6's are not necessarily at the both ends of the main axis (2)-(3) of the connected 60-hedra and point (3), for example, can be inside of 60hedron ((2)-(4)). By this, the diameter is smaller and all the mapped points can be inside the gazing crystal. 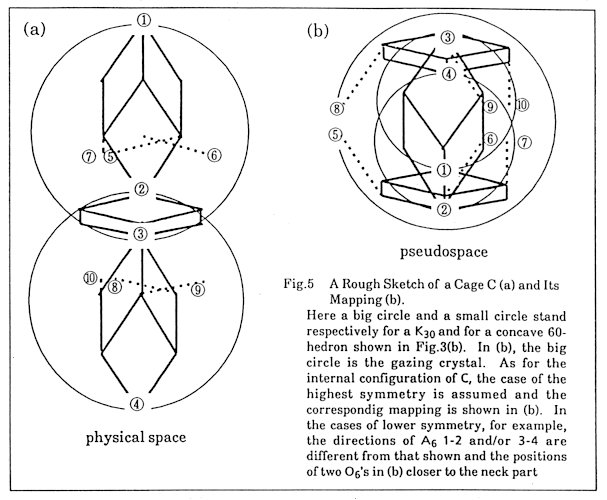 Fig. 5 In the gazing crystal, an available arrangement of two O6's and points (5)-(10) is uniquely determined for any position of the connected 60-hedron as easily seen from that the projection is deterministic. The arrangement of the internal points in a cage is uniquely determined according to the circumstance of a cage so that no simple repeat of the same unit cells. This is the most striking feature of the model. Its local symmetry is not so high as can be seen from the fact that A6* never be trigonal, but it is rather uniform. From these investigations, the following
can be concluded
In the transformation model, the hierarchy
of symmetry can be designed by making use of its freedom. Start with a
flower dodecahedron Fl60 which is the only configuration with
full icosahedral symmetry among all the compound of A6's and
O6's. Apply the Penrose transformation to this. The original
Fl60 is kept unchanged and 20 F20's are put on the
20 flower faces. Fivefold symmetry and therefore icosahedral symmetry can
not be kept since a F20 does not have 5-fold symmetry as easily
seen from the fact that it has four internal points. However, there are
some configurations with symmetry belonging to the symmetry group Th
and T which are both subgroup of the group Ih.
For the cage parts, trigonal symmetry can be kept. The same cage configuration
can be always used. In such a case, system has a kind of chirality. By
defining some rank for the centres of Fl60's, the hirarchical
symmetry of
Th or T is realizable.
|