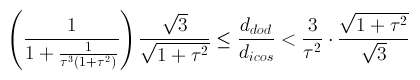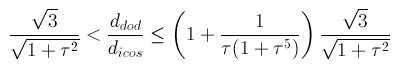= 1+1/3τ4
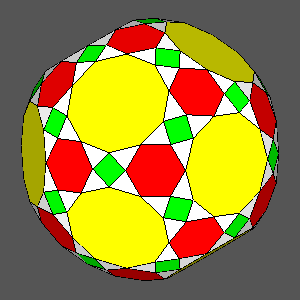
= 1.0486, the solid obtained starting from RID includes regular decagonal faces of dodecahedron
when dRT = 1+1/τ5 = 1.0902,
one obtains a (non Archimedean) truncated icosahedron, with the faces of the rhomb-triacontahedron tangent to thirty of its edges.
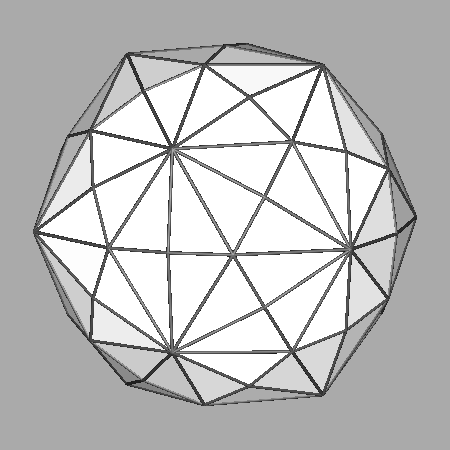
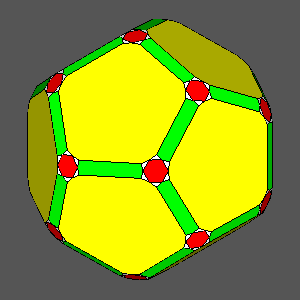
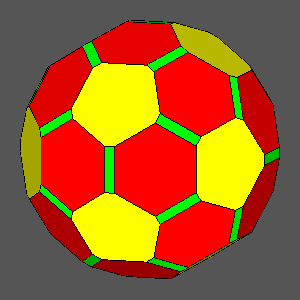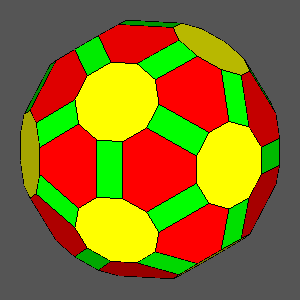
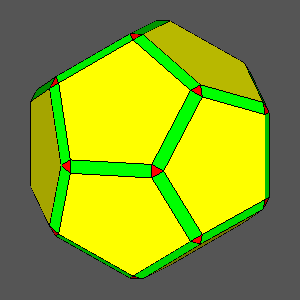
The other Archimedean solid which can be obtained by the intersection of dodecahedron, icosahedron and rhomb-triacontahedron
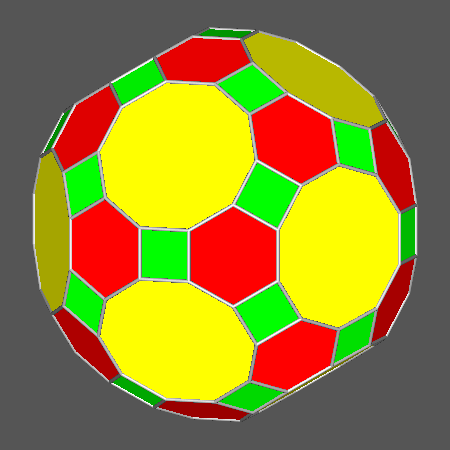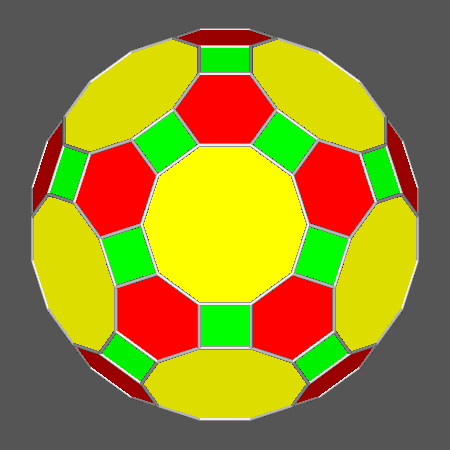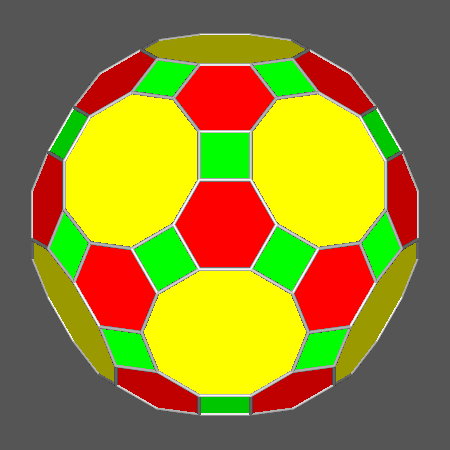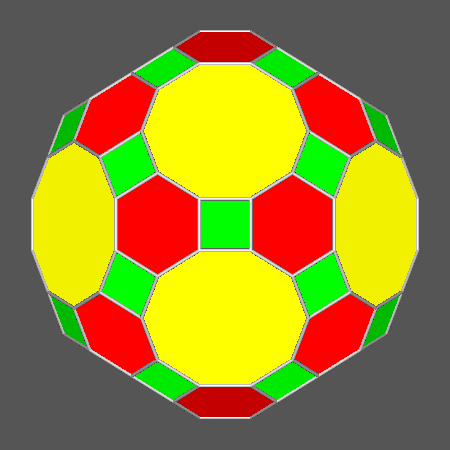
is the Archimedean truncated icosidodecahedron
(tID), shown in
Fig. 3b; its faces, all regular,
consist of decagonal faces of dodecahedron, hexagonal faces of icosahedron and square faces of rhomb-triacontahedron.
In case of the
tID, the values of the ratios of the central distances are:
and:
(As one can see, in
RID and
tID the ratio
dicos /dRT assumes the reciprocal values
(5-2τ)/√3
and √3/(5-2τ)
respectively, analogously to what happens with the ratio
doct /dRD in RCO and tCO)
Assigning also in this case the value dRT = 1
to the central distance of the rhomb-triacontahedron, it follows that the central distances of the other forms, whose intersection
with RT generates the Archimedean truncated icosidodecahedron tID, are:
dicos
= √3/(5-2τ) = 0.9819
and ddod =
5/((3τ-2)√1+τ2)
= 0.9210
Letting unchanged the ratio ddod /dicos
and varying only dRT :
an increase of the value of dRT
from 1 to = 1+1/(τ(τ5+1)) = 1.0511 leads to a (non-Archimedean) truncated icosahedron,
with the faces of the rhomb-triacontahedron tangent to thirty of its edges
a decrease of the value of dRT
from 1 to = 1-1/(2(τ5+1)) = 0.9586
leads to a vertex-transitive polyhedron in which each vertex is shared by a pentagonal face of dodecahedron,
an equilateral triangular face of icosahedron and two rectangular faces of rhomb-triacontahedron:
its dual consists in the deltoid-hexecontahedron
{4τ-5 1 0} (whereas the rather similar Catalan deltoid-hexecontahedron
{1+1/τ2 1 0} is the dual of RID).
The data relative to the solids deriving from RID and tID are resumed in Table B.
|
Archimedean truncated icosidodecahedron
(tID), rhomb-icosidodecahedron (RID) and solids including regular faces,
obtained by varying the central distance of the intersecting rhomb-triacontahedron |
| |
RID |
tID |
| ddod /dicos |
_su_d(icos)_RID_x_tab_.gif) |
_su_d(icos)_tID_xtab_.gif) |
| dicos /dRT |
_su_d(RT)_RID_xtab.gif) |
_su_d(RT)_tID_xtab.gif) |
|
If dRT =1: |
|
| dicos |
_su_d(RT)_RID_xtab.gif) |
_su_d(RT)_tID_xtab.gif) |
| ddod |
_RID_.gif) |
_tID_x_tab.gif) |
| Indices of the Catalan duals |
{1+1/τ2 1 0} |
{2 3/τ 1}
|
In each Catalan solid, the dihedral angles between all the couples of contiguous faces are equal and measure: |
25.879° |
15.112° |
| |
|
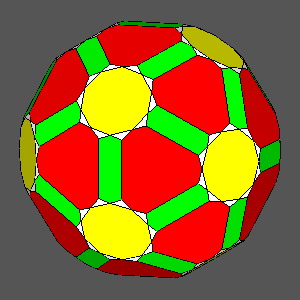
Vertex-transitive solids including regular hexagonal faces
of icosahedron |
|
|
dRT |
_RID_hexagonal_faces.gif) |
1 |
| Indices of the dual hexakis-icosahedra |
{3(1+1/τ2) 3 2/τ2} |
{2 3/τ 1}
|
|
In each dual, the six dihedral angles between contiguous faces sharing a vertex along [111] are equal and measure:
|
16.981° |
15.112° |
| |
|
Vertex-transitive solids including regular decagonal faces of dodecahedron |
|
|
dRT |
_RID_decagonal_faces.gif) |
1 |
| Indices of the dual hexakis-icosahedra |
{5 5/(1+1/τ2)
2/τ2} |
{2 3/τ 1}
|
In each dual, the ten dihedral angles between contiguous faces sharing a vertex along [τ01] are equal and measure:
|
14.112° |
15.112° |
| |
|
Vertex-transitive solids including regular pentagonal faces of dodecahedron and equilateral triangular faces of icosahedron
(in RID also the faces of rhomb-triacontahedron are square) |
|
|
dRT |
1 |
_tID_to%20DH.gif) |
| Indices of the dual deltoid-hexecontahedra |
{1+1/τ2 1 0} |
{4τ-5 1 0} |
|
In each dual, the three dihedral angles between contiguous faces sharing a vertex along [111] are equal
(due to the 3-fold axis) and measure:
|
25.879° |
22.954° |
|
In each dual, the five dihedral angles between contiguous faces sharing a vertex along
[τ01] are equal (due to the 5-fold axis) and measure:
|
25.879° |
27.769° |
| |
|
Non-Archimedean truncated icosahedra deriving from RID and tID
by increasing the value of dRT |
|
| dRT |
_RID_to%20tI.gif) |
_tID_to%20tI.gif) |
| Indices of the dual pentakis-dodecahedra |
{τ5+1 0 1} |
{3 0 1/τ4} |
|
In each dual, the five dihedral angles between contiguous faces sharing a vertex
along [τ01] are equal (due to the 5-fold axis) and measure:
|
30.942° |
33.042° |
Table B
The ultimate vertex-transitive solids resulting from the intersection of each Archimedean solid with the rhomb-triacontahedron (RT)
are shown in Fig. 4 (a further decrease of dRT would lead to solids
whose vertices are no more shared by couples of triangular and pentagonal faces).
The comparison between each of such vertex-transitive solids and the rhomb-icosidodecahedron (RID) shown in Fig.3a
reveals that the rectangular faces deriving from RT become square in the RID, being it an Archimedean solid.
|
Forms including faces having the shape of regular pentagons and equilateral triangles,
derived from the intersection between a rhomb-triacontahedron (RT) and each of four Archimedean polyhedra with icosahedral symmetry
|
 |
 |
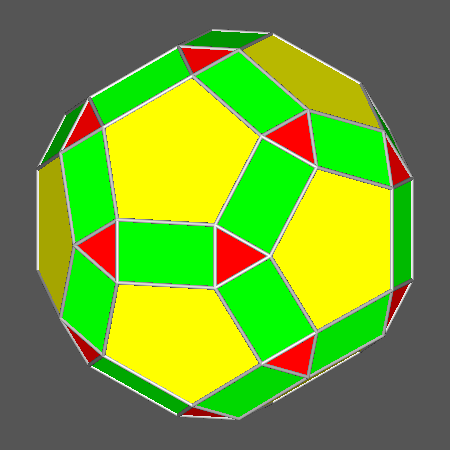
Vertex transitive solid deriving from the
intersection of RT with the Archimedean truncated icosahedron (in
which ddod =
(1+1/3τ 2 )/√ 1+1/τ2 and
dicos = τ/√ 3)
when dRT = (τ+4)/6.
Its dual is the
deltoid-hexecontahedron {τ+1/τ 2 0} |
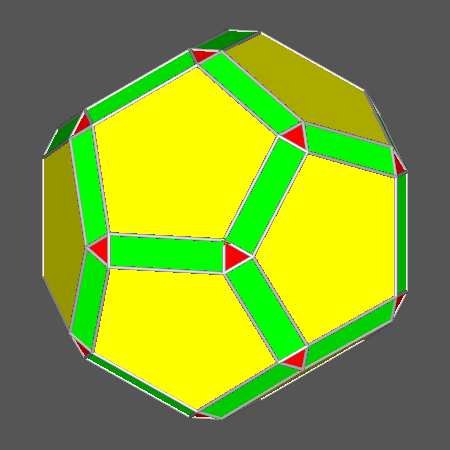
Vertex transitive solid deriving from the Archimedean
truncated icosidodecahedron (tID) when the value of dRT decreases from
1 to 1-1/(2(τ5+1)),
whereas the values of ddod and dicos do not change:
ddod = 5/((3τ-2)√1+τ2)
and dicos = √3/(5-2τ)
Its dual is the
deltoid-hexecontahedron {4τ-5 1 0} |
 |
 |
Vertex transitive solid deriving from the intersection of RT with the icosi-dodecahedron ID (in
which ddod = 1 /√ 1+1/τ2 and
dicos =
τ/√ 3)
when dRT = (τ2+1)/4.
Its dual is the
deltoid-hexecontahedron {τ10} |
Vertex transitive solid deriving from the
intersection of RT with the Archimedean truncated
dodecahedron AtD (in
which ddod = 1/√ 1+1/τ2
and dicos = (1+1/(τ 5+τ 3))τ/√ 3 when dRT = (4τ+3)/10.
Its dual is the
deltoid-hexecontahedron {210} |
Fig. 4
Fig. 5 shows the views along the [111] direction of the solids, obtained by the intersection of dodecahedron, icosahedron and
rhomb-triacontahedron, which include regular hexagonal faces (as the Archimedean truncated icosahedron, already shown in Fig. 2a).
|
View along the [111] direction of forms, having icosahedral symmetry, derived from the intersection of Archimedean polyhedra
with a rhomb-triacontahedron and including regular hexagonal faces, compared with the Archimedean truncated icosidodecahedron
|
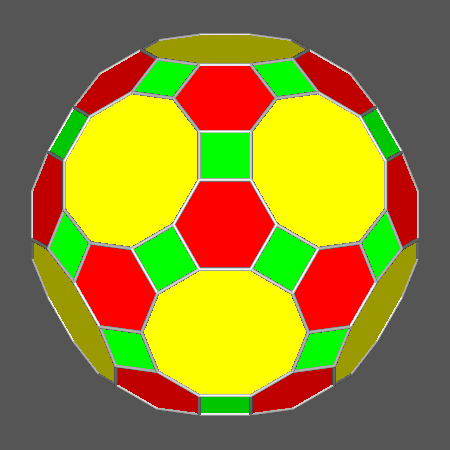 |
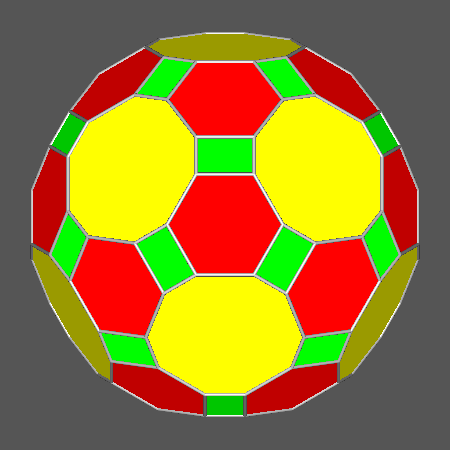 |
|
Archimedean truncated icosi-dodecahedron |
Polyhedron with regular hexagonal faces derived from the rhomb-icosidodecahedron (RID)
by increasing the central distance of the faces of rhomb-triacontahedron, but letting unchanged the ratio
ddod /dicos |
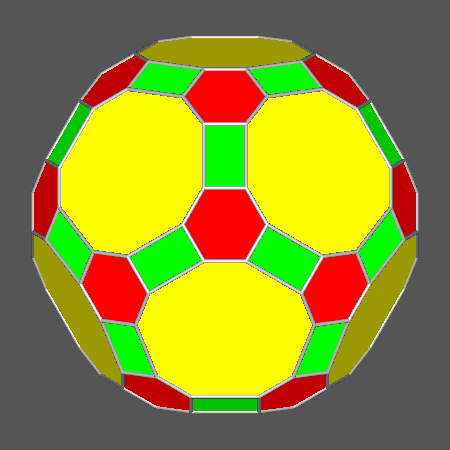 |
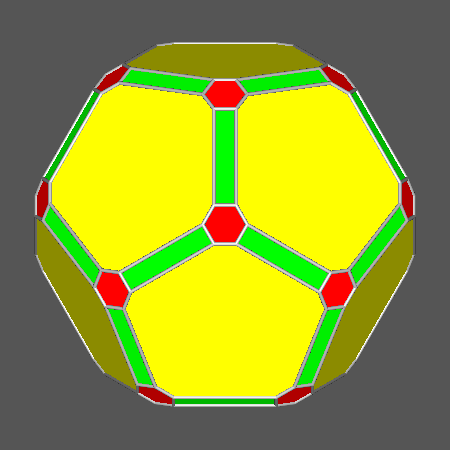 |
|
Polyhedron including regular hexagonal faces derived from the truncation by a rhomb-triacontahedron of the Archimedean icosidodecahedron |
Polyhedron including regular hexagonal faces
derived from the truncation by a rhomb-triacontahedron of the Archimedean truncated dodecahedron |
Fig. 5
Fig. 6 shows the views, along the [τ01] direction, of the solids, obtained by the intersection of
dodecahedron, icosahedron and rhomb-triacontahedron, which include regular decagonal faces (as the Archimedean truncated
dodecahedron already shown in Fig. 2b).
|
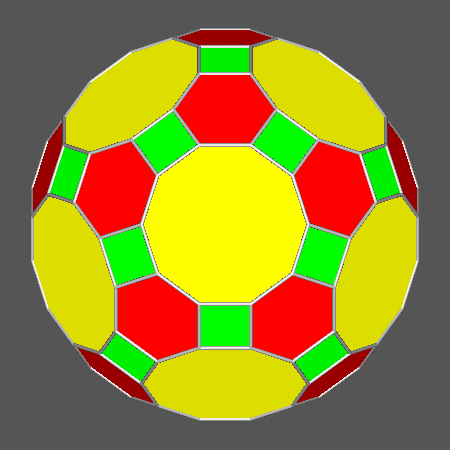
View along the [τ01] direction of
forms, having icosahedral symmetry, derived from the intersection of Archimedean polyhedra
with a rhomb-triacontahedron and including regular hexagonal faces,
compared with the Archimedean truncated icosi-dodecahedron |
 |
 |
|
Archimedean truncated icosi-dodecahedron (tID) |
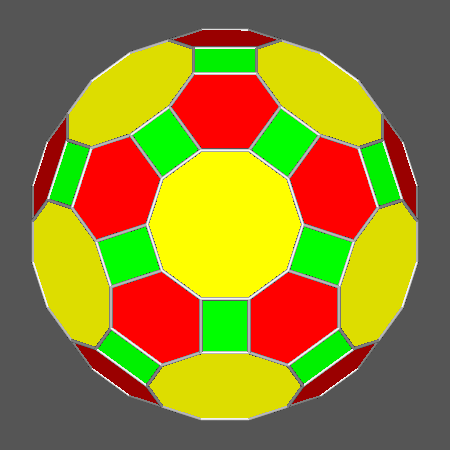
Polyhedron including regular decagonal faces derived from
the rhomb-icosidodecahedron (RID) by increasing the central distance of the faces of rhomb-triacontahedron,
but letting unchanged the ratio ddod /dicos |
 |
 |
|
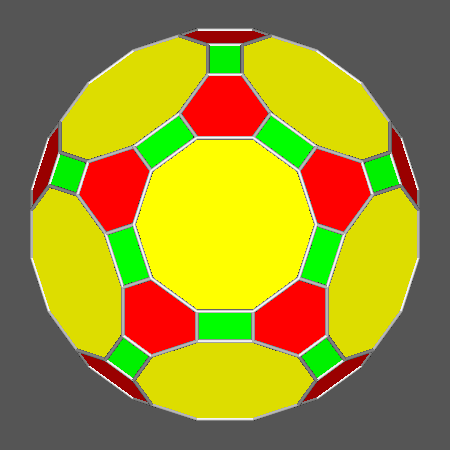
Polyhedron including regular decagonal faces, derived from
the truncation of the icosidodecahedron by a rhomb-triacontahedron |
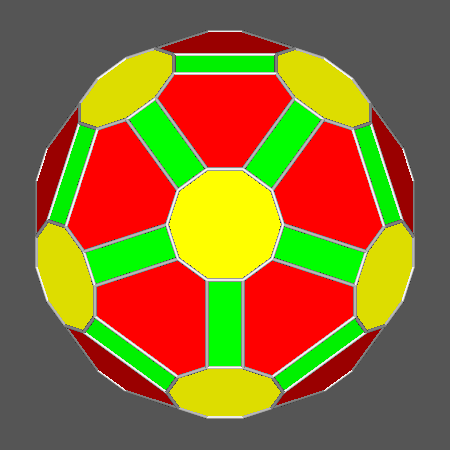
Polyhedron including regular decagonal faces, derived from
the truncation by a rhomb-triacontahedron of the Archimedean truncated icosahedron |
Fig. 6
In Fig. 7 the Archimedean truncated icosidodecahedron (tID) is
compared to the rather similar solids which include regular faces having the
shape of hexagons or decagons, obtained starting from two Archimedean solids,
the icosidodecahedron (ID) and the rhomb-icosidodecahedron (RID), by a proper
variation of the central distance of the rhomb-triacontahedron dRT.
|
Truncated icosidodecahedron (tID)
compared with the four similar polyhedra including regular hexagonal or
decagonal faces, obtained by intersecting the rhomb-icosidodecahedron (RID)
and the icosi-dodecahedron (ID) with a rhomb-triacontahedron (RT) |
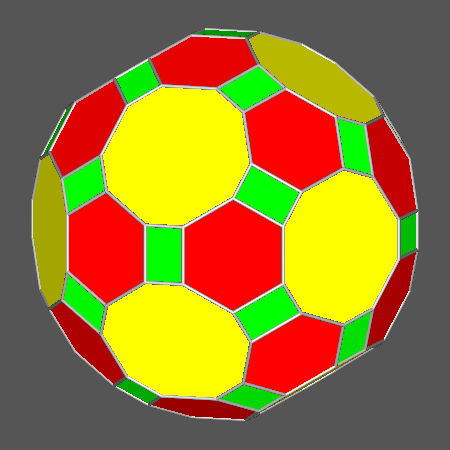 |
 |
|
Polyhedron including regular hexagonal faces of icosahedron, derived from RID
by a proper increase of the central distance dRT |
Polyhedron including regular decagonal faces of dodecahedron, derived from RID
by a proper increase of the central distance dRT
|
|
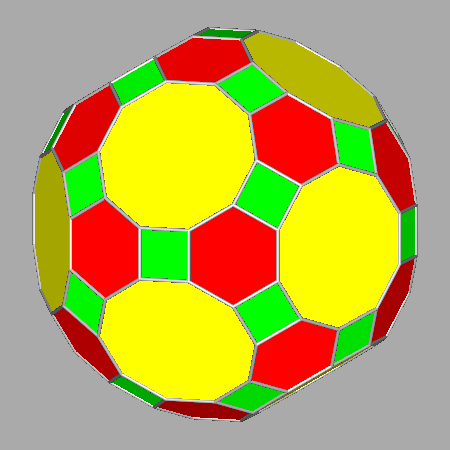 |
|
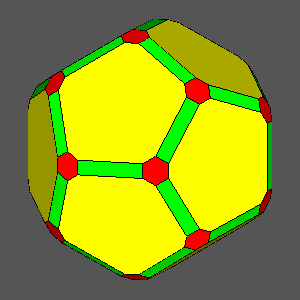
Being an Archimedean solid, the truncated
icosidodecahedron (tID) includes only regular faces:
twelve decagonal faces of dodecahedron, twenty hexagonal faces of
icosahedron and thirty square faces of rhomb-triacontahedron |
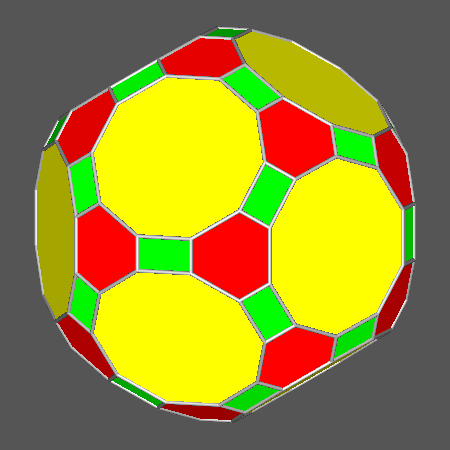 |
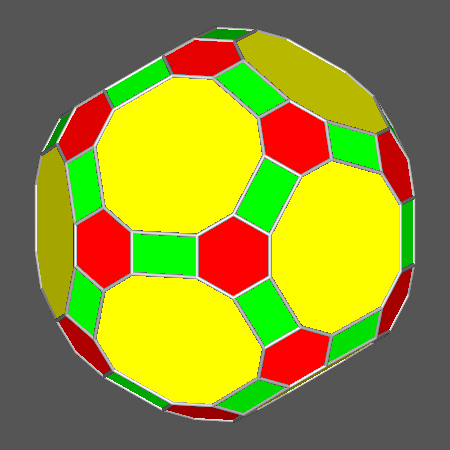 |
|
Polyhedron including regular decagonal faces of dodecahedron, derived from ID by a proper
decrease of the central distance dRT
|
Polyhedron including regular hexagonal faces
of icosahedron, derived from ID by a proper decrease of the central distance dRT |
Fig. 7
The hexakis-octahedra dual of the solids reported in Fig. 7 are shown in the following Fig. 8.
|
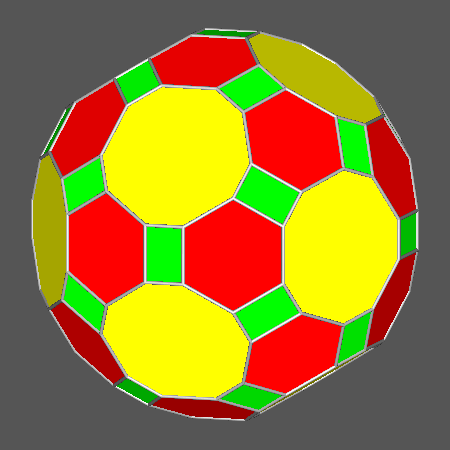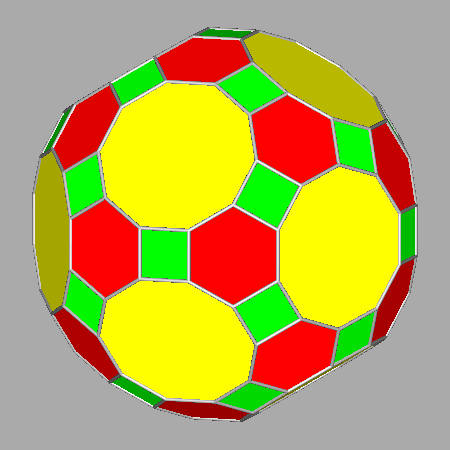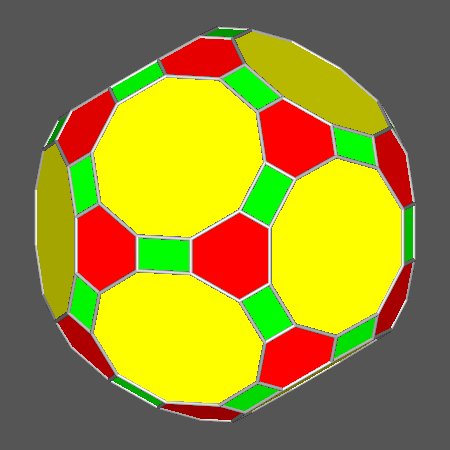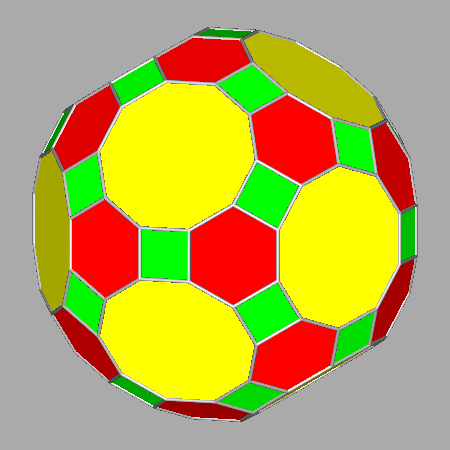
Comparison between the Catalan hexakis-icosahedron, dual of
the Archimedean truncated icosidodecahedron (tID), and four very similar hexakis-icosahedra,
dual of polyhedra, derived from ID and RID, which include regular hexagonal or decagonal faces |
 |
 |
|
Hexakis-icosahedron {3(1+1/τ2) 3 2/τ2},
dual of the solid, derived from RID, which include regular hexagonal faces.
The six dihedral angles between each couple of contiguous faces sharing a vertex along the [111] axis measure
16.980° |
Hexakis-icosahedron {5 5/(1+1/τ2)
2/τ2},
dual of the solid, derived from RID, which include regular decagonal faces.
The ten dihedral angles between each couple of contiguous faces sharing a vertex along the
[τ01] axis measure 14.112° |
|
 |
|
Hexakis-icosahedron {2 3/τ 1},
dual of the Archimedean truncated icosahedron (tID): as it is a Catalan solid, all the dihedral angles
between each couple of edge-sharing faces are equal and measure = 15.112° |
 |
 |
|
Hexakis-icosahedron {τ11}, dual of the solid derived from ID which includes regular decagonal faces.
The ten dihedral angles between each couple of contiguous faces, sharing a vertex along the [τ01] axis, measure 16.535° |
Hexakis-icosahedron {τ1τ3},
dual of the solid derived from ID which includes regular hexagonal faces.
The six dihedral angles between each couple of contiguous faces, sharing a vertex along the [111] axis, measure 12.363°
|
Fig. 8
In order to highlight the small differences among the images of the solids shown in Fig. 7 and Fig. 8,
the corresponding animated sequences have been reported in Fig. 9.
 |
 |
|
Animated sequence highlighting the differences between the truncated icosidodecahedron (tID) and the solids,
including hexagonal or decagonal regular faces, derived from the rhomb-icosidodecahedron (RID) and the icosidodecahedron (ID)
|
Animated sequence highlighting the small differences between the Catalan hexakis-icosahedron, dual of tID,
and the other hexakis-icosahedra, which are the duals of solids,
including hexagonal or decagonal regular faces, derived from ID and RID. |
Fig. 9
As already shown in a previous paper [4], the intersection of the Archimedean truncated
icosahedron with its dual, the Catalan hexakis-icosahedron {2 3/τ 1},
can generate an interesting solid, in turn including regular decagonal faces of dodecahedron, regular hexagonal faces of icosahedron
and square faces of rhomb-triacontahedron as the Archimedean tID, whereas the faces coming from the dual Catalan hexakis-icosahedron
have the shape of scalene triangles.
In Fig. 10 such solid is compared with the four solids resulting from the
intersection of the couples of dual polyhedra, derived from ID and RID,
which have been reported in Fig. 7 and Fig. 8: also these four solids include hexagonal or decagonal regular faces.
|
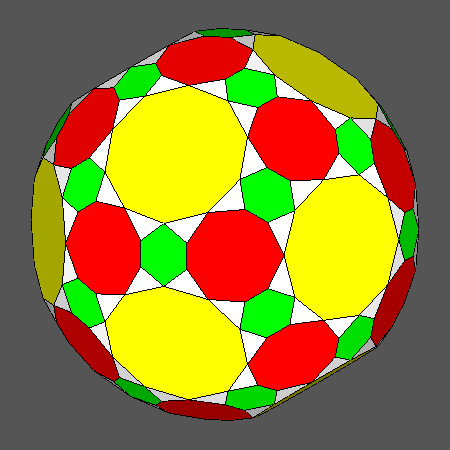
Comparison between the intersection of tID with the dual Catalan
hexakis-icosahedron and the intersection, with the relative duals, of the polyhedra,
derived from the Archimedean ID and RID, which include hexagonal or decagonal regular faces |
 |
 |
|
Solid resulting from the intersection with its dual of the polyhedron, derived from RID,
which includes
regular hexagonal
faces of icosahedron |
Solid resulting from the intersection with its dual of the polyhedron, derived from RID,
which includes
regular decagonal faces of dodecahedron |
|
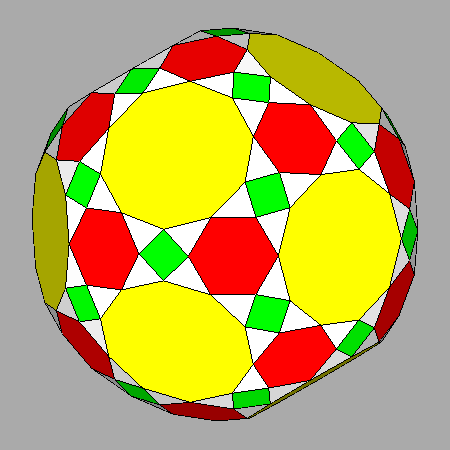 |
|
Solid resulting from the intersection between the Archimedean truncated
icosidodecahedron (tID)
and the dual Catalan hexakis-icosahedron, including
square,
regular hexagonal
and regular decagonal faces |
|
|
 |
|
Solid resulting from the intersection with its dual of the polyhedron, derived from ID,
which includes regular decagonal faces of dodecahedron |
Solid resulting from the intersection with its dual of the polyhedron, derived from ID,
which includes regular hexagonal faces of icosahedron |
Fig. 10
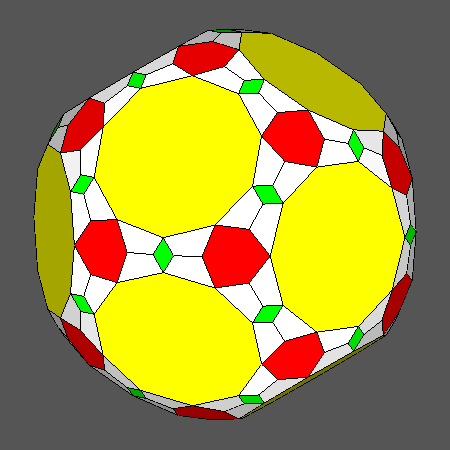
The solid resulting from the intersection of tID with its dual, the Catalan hexakis-icosahedron,
is clearly not vertex-transitive, but its vertices are all equidistant from the barycenter.
Therefore a further dual of such solid includes faces which are different but equidistant from the barycenter;
in addition, the following series of dihedral angles are egual:
the six dihedral angles between contiguous faces sharing a vertex along [111]
the ten dihedral angles between contiguous faces sharing a vertex along [τ 01]
the four dihedral angles between contiguous faces sharing a vertex along [100]
In Fig. 11 this solid is compared with four similar solids, derived from ID and
RID,
which in turn are the duals of the solids reported in Fig. 10.
|
Duals of the polyhedra obtained from the intersection
between solids including regular faces derived from Archimedean polyhedra and the relative duals |
_.png) |
_.png) |
|
Solid derived from RID, in which all the six
dihedral angles between each couple of contiguous faces sharing a vertex along [111] measure 14.856° |
Solid derived from RID, in which all the ten dihedral angles
between each couple of contiguous faces sharing a vertex along [τ01] measure 13.521° |
|
_450px.png) |
|
Solid, consisting of the
deltoid-hexecontahedron {4τ-5 1 0} and of the couple of symmetric forms:
triakis-icosahedron {4τ+1 1 0} and
pentakis-dodecahedron {4τ+1 0 1}, which is the dual of the polyhedron
obtained by the intersection of the Archimedean truncated icosahedron with its dual, the Catalan hexakis-icosahedron.
In such solid:
the 6 dihedral angles between contiguous faces sharing a vertex along [111] measure 13.193°
the 10 dihedral angles between contiguous faces sharing a vertex along [τ01] measure 14.495°
the 4 dihedral angles between contiguous faces sharing a vertex along [100] measure 10.764° |
_.png) |
_bis_white_faces.png) |
|
Solid derived from ID, in which all the ten dihedral angles between each couple of contiguous faces
sharing a vertex along [τ01] measure 15.887° |
Solid derived from ID, in which all the six dihedral angles between each couple of contiguous faces sharing a vertex
along [111] measure 10.764° |
Fig. 11
In order to highlight the differences among the images of the solids shown in Fig. 10 and Fig. 11,
the corresponding animated sequences have been reported in Fig. 12.
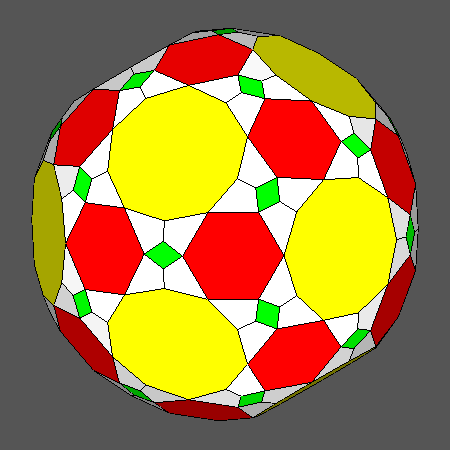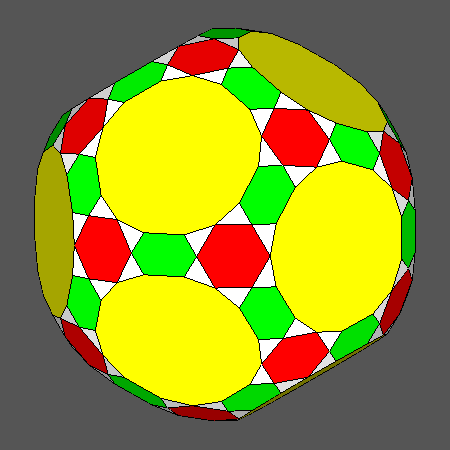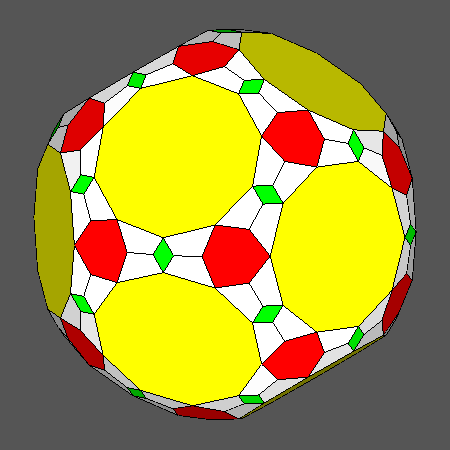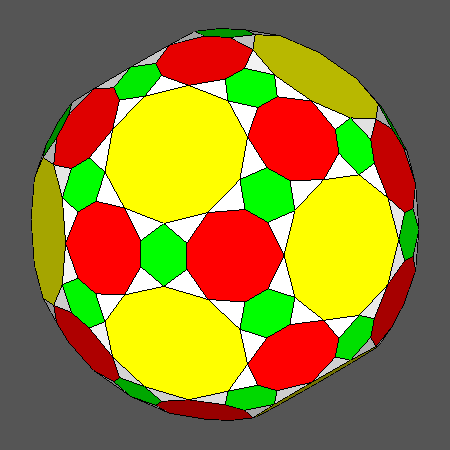 |
 |
|
Animated sequences highlighting the differences which characterize the solids reported in Fig. 10 and Fig. 11 |
Fig. 12
The first row of Fig. 13 shows, in the center, the Archimedean truncated icosidodecahedron (tID)
compared with the solids including regular hexagonal or decagonal faces, derived from the intersection with a rhomb-triacontahedron
of the Archimedean truncated dodecahedron (AtD) and truncated icosahedron (AtI), respectively.
The relative duals are reported in the second row, whereas the third row shows the polyhedra, including regular faces,
which result from the intersections of each dual couple of solids reported in the first two rows;
finally the duals of the solids belonging to the third row are shown in the fourth row.
|
Archimedean truncated icosidodecahedron (tID) compared with the polyhedra, including regular faces,
which derive from the truncation
by a rhomb-triacontahedron of the Archimedean truncated dodecahedron (AtD) and truncated icosahedron (AtI),
followed by their duals and other related forms |
 |
 |
 |
|
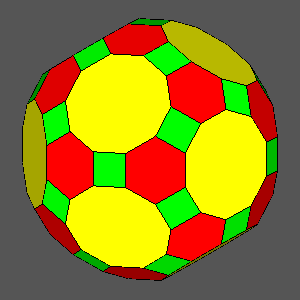
Polyhedron with regular hexagonal faces derived from the Archimedean truncated dodecahedron
(AtD) |
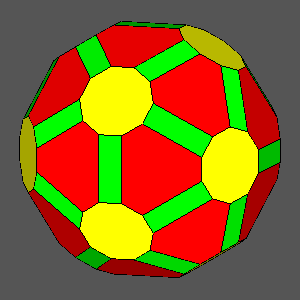
Archimedean truncated icosidodecahedron (tID) consisting of regular hexagonal, regular decagonal and square faces |
Polyhedron with regular decagonal faces derived from the Archimedean truncated icosahedron
(AtI) |
 |
 |
 |
|
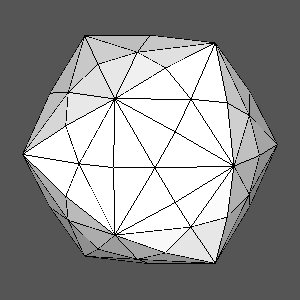
Hexakis-icosahedron {2 1 1/(3τ2)}, dual of the solid with
regular hexagonal faces deriving from AtD |
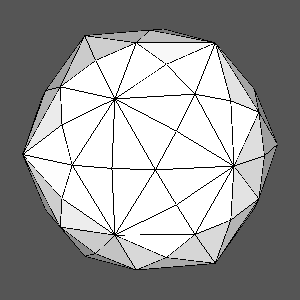
Catalan hexakis-icosahedron {2 3/τ 1}, dual of tID |
Hexakis-icosahedron {4τ-1 5-τ 2}, dual of the solid with regular
decagonal faces deriving from AtI |
 |
 |
 |
|
Solid including regular hexagonal faces, obtained from the intersection of the polyhedron deriving from AtD with its dual |
Solid resulting from the intersection of tID with its dual |
Solid including regular decagonal faces, obtained from the intersection of the polyhedron deriving from AtI with its dual
|
_300px.png) |
_300px.png) |
_300px.png) |
|
Solid, dual of the intersection of the polyhedron deriving from AtD with its dual, in which the dihedral angles between the six couples of contiguous faces sharing a vertex along [111]
measure 5.653° |
Solid dual of the intersection between tID
and the dual Catalan hexakis-icosahedron (the values of the dihedral angles have already been reported in Fig.
11) |
Solid, dual of the intersection of the polyhedron deriving from AtI with its dual, in which the dihedral angles between the ten couples of contiguous faces sharing a vertex
along [τ01] measure 10.054° |
Fig. 13
Solids including regular-shaped faces can be obtained also by the
intersection with a rhomb-triacontahedron (RT) of whichever
non-Archimedean truncated icosahedron (tI) or truncated dodecahedron (tD).
Starting from any situation in which RT is tangent to thirty edges of tI or tD,
by decreasing its central distance dRT
one obtains always, in the early stages, vertex-transitive polyhedra, whose duals are hexakis-icosahedra.
Afterwards, when dRT decreases to a proper value,
the truncation of each tI and tD by RT
leads to a different kind of vertex-transitive polyhedron, whose dual is a deltoid-hexecontahedron; as already shown
relatively to the isomorphic solids reported in Fig.4, each vertex is shared by a regular pentagon, an equilateral triangle and, usually, two rectangles.
Concerning the possibility to get, at intermediate steps of the truncation process by RT, other solids including regular faces,
one must distinguish among different intervals of values of the ratio
ddod /dicos:
when (1+1/(3τ2))
√3/√
1+τ2 ≤
ddod /dicos<
(1+1/τ2)√3
/√1+τ2,
the intersection of each truncated icosahedron with RT can generate a solid including regular decagonal faces of dodecahedron
(the ratio ddod /dicos
= (1+1/τ2)√3
/√1+τ2
= (√1+1/τ2)
√3/τ
is relative to the icosahedron, whereas the ratio ddod /dicos=
(1+1/3τ2)√3
/√1+τ2
is relative to the Archimedean truncated icosahedron AtI which, in turn,
itself includes regular hexagonal faces of icosahedron)
when (1+1/(τ(τ5+1)))√
3/√1+τ2
< ddod
/dicos<
(1+1/3τ2)√3
/√1+τ2, the intersection of each truncated
icosahedron with RT generates, in sequence, two solids including hexagonal or decagonal regular faces
when (1+1/(3τ5))√3/√1+τ2
< ddod /dicos
≤ (1+1/(τ(τ5+1)))√3/√1+τ2,
three are the solids including regular faces which can be sequentially generated from the intersection
of each truncated icosahedron with RT:
the two solids including regular hexagonal faces of icosahedron or regular decagonal faces of dodecahedron
are followed by a solid including square faces of RT
(if ddod /dicos
= (1+1/(τ(τ5+1)))√3/√1+τ2,
such solid is the Archimedean rhomb-icosidodecahedron which, together with square faces of rhomb-triacontahedron,
includes also equilateral triangular faces of icosahedron and regular pentagonal faces of dodecahedron)
when ddod /dicos =
(1+1/(3τ5))(√3
/√1+τ2),
in coincidence with an unique value dRT of its central distance,
the intersection of the rhomb-triacontahedron with the truncated icosahedron leads to the Archimedean truncated icosidodecahedron,
which include simultaneously regular faces of three kinds, having the shape of hexagons, decagons and squares
when √3
/√1+τ2
< ddod
/dicos
< (1+1/(3τ5))(√3
/√1+τ2),
the three solids including regular faces are obtained in an inverse order, since the solid including square faces of rhomb-triacontahedron
comes before the solid with regolar decagonal faces, followed at last by the solid with regular hexagonal faces
when (√3
/√1+τ2)
/(1+1/(τ3(τ2+1)))
< ddod /dicos
≤√3/√1+τ2,
from the intersection between RT and each truncated dodecahedron (or the icosi-dodecahedron ID,
if ddod /dicos=
√3/√1+τ2)
firstly one obtains a solid with regular decagonal faces of dodecahedron, and then a solid with regular hexagonal faces of icosahedron
when (√3
/√1+τ2)
/(1+1/τ4) <
ddod /dicos
≤ (√3/√1+τ
2)/(1+1/(τ3
(τ2+1))),
the intersection of each truncated dodecahedron with RT can generate a solid including regular hexagonal faces of icosahedron
(the ratio ddod /dicos=
(√3/√1+τ2)
/(1+1/τ4) =
(τ/√3)/(√1+1/τ2)
is relative to the dodecahedron, whereas the ratio ddod
/dicos = (√3
/√1+τ2)
/(1+1/(τ3(τ2+1)))
is relative to the Archimedean truncated dodecahedron AtD which, in turn,
itself includes regular decagonal faces of dodecahedron).
A series of solids including regular-shaped faces, obtained sequentially by the intersection with RT of
selected non Archimedean truncated icosahedra tI or truncated dodecahedra tD belonging to the six intervals just defined,
is visualized in Fig. 14.
|
Solids which include
faces having the shape of regular polygons, obtained by the intersection
with the rhomb-triacontahedron of generic non-Archimedean truncated icosahedra and
truncated dodecahedra, compared with the Archimedean truncated icosidodecahedron |
|
Truncated icosahedra
and truncated dodecahedra |
Vertex-transitive solids which include regular faces having hexagonal, decagonal or square shape |
Vertex-transitive solids, dual of deltoid-hexecontahedra, which include
regular faces having the shape of pentagons and triangles |
|
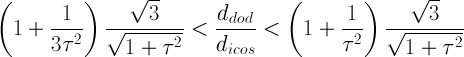
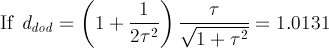
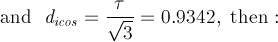 |
 |
 |
 |
|
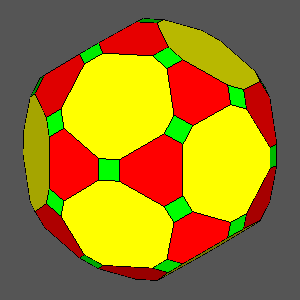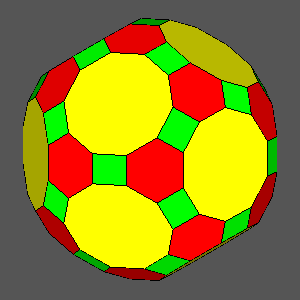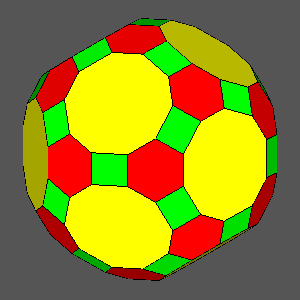
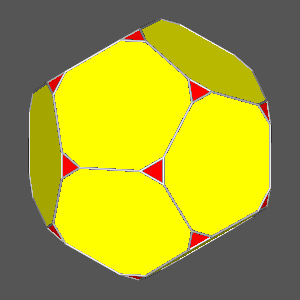
dRT = 1 |
dRT = 0.9736:
decagonal regular faces |
dRT = 0.9523 |
|
|
|
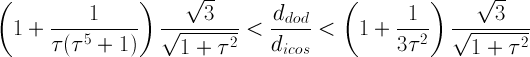
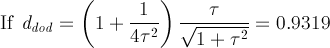
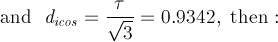 |
 |
 |
 |
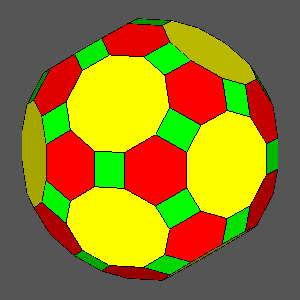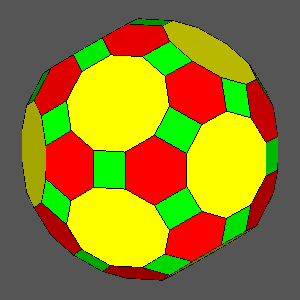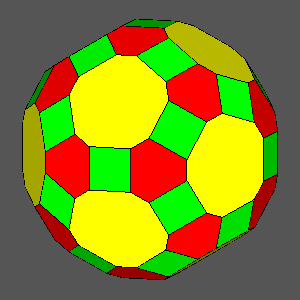
|
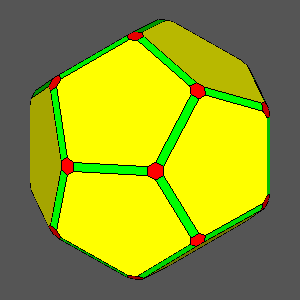
dRT
= 1 |
dRT
= 0.9841: hexagonal regular faces
dRT
= 0.9604: decagonal regular faces |
dRT = 0.9284 |
| |
|
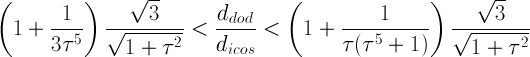
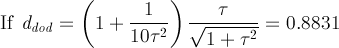
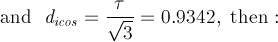 |
 |
 |
 |
|
dRT = 1 |
dRT = 0.9554 : hexagonal regular faces
dRT = 0.9525 : decagonal regular faces
dRT = 0.9382 : square faces |
dRT = 0.9141 |
| |
|
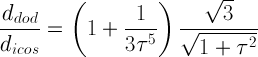 |
 |
 |
 |
|
b)
An increase of the value of dRT from 1 to 3/(3τ-2) =
1+1/(τ(τ5+1))
= 1.051 implies that the rhomb-triacontahedron is tangent to thirty edges of a truncated icosahedron in which the ratio
ddod /dicos
derive from the same ddod and
dicos values relative to tID
|
a)
If, in addition to such value of the ratio ddod /dicos,
the ratio dicos /dRT
assumes the value √3/(5-2τ),
the result of the truncation by RT is the Archimedean truncated icosi-dodecahedron (tID).
If one assumes dRT = 1, it follows that:
dicos =
√3/(5-2τ),
ddod =
5/((3τ-2)√1+τ2)
|
c)
Letting unchanged the values of ddod
and dicos relative to tID,
a decrease of the value of dRT
from 1 to (3τ+4)/(2(τ+3) = 1- 1/(2(τ5+1))
= 0.959 leads to a vertex transitive solid, dual of the deltoid-hexecontahedron
{4τ-5 1 0}, in which each vertex is shared by four faces
|
|
a)
Alternatively, when dRT = 1 the faces of the rhomb-triacontahedron
are tangent to thirty edges of the truncated icosahedron tI in which the same ratio
ddod /dicos derive from:
ddod=
5/(3√1+τ2) and
dicos=
τ/√3
|
b)
Letting unchanged the values of ddod and dicos relative
to the truncated icosahedron tI,
a decrease of the value of dRT from
1 to (3τ-2)/3 = 1- 1/(3τ4) = 0.951 leads to tID
|
c)
Letting unchanged the values of ddod and dicos
relative to the truncated icosahedron tI,
a decrease of the value of dRT
from 1 to 1- (7-4τ)/6 = 0.912
leads to the dual of the deltoid-hexecontahedron {4τ-5 1 0} |
|
|
|

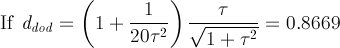
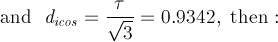 |
 |
 |
 |
|
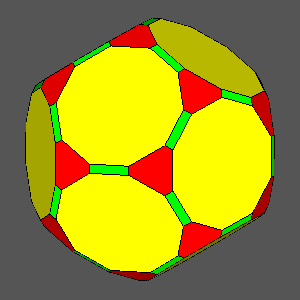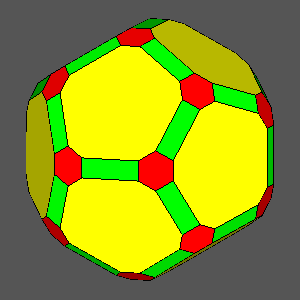
dRT
= 1 |
dRT
= 0.9691 : square faces
dRT
= 0.9499 : decagonal regular faces
dRT
= 0.9459 : hexagonal regular faces |
dRT = 0.9093 |
|
|
|
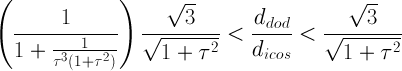
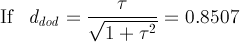
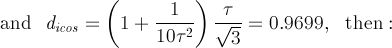 |
 |
 |
 |
|
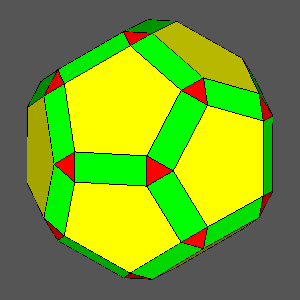
dRT
= 1 |
dRT
= 0.9781 : decagonal regular faces
dRT
= 0.9530 : hexagonal regular faces |
dRT = 0.9295 |
|
|
|
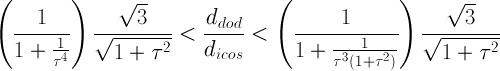
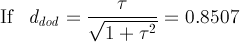
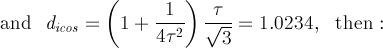 |
 |
 |
 |
|
dRT
= 1 |
dRT
= 0.9780 : hexagonal regular faces |
dRT = 0.9670 |
Fig. 14
So it has been shown that solids including some kind of regular-shaped face can be obtained starting from each truncated icosahedron or dodecahedron in
correspondence of different values of the central distance dRT of the rhomb-triacontahedron.
The relations resumed in Table C hold between dRT
and the couple of central distances ddod of dodecahedron
and dicos of icosahedron
(as the ratio ddod /dicos
varies in well defined ranges), and characterize all the polyhedra
belonging to each series of solid which include one or two kinds of regular-shaped faces.
|
Relations holding between the central distance of a truncating rhomb-triacontahedron
and the central distances of dodecahedron and icosahedron belonging to the solid to be truncated,
in case of each series of vertex-transitive solids including a certain kind of regular faces |
|
The regular faces of the series of solids are pentagonal faces of dodecahedron and triangular equilateral faces of icosahedron if:
when the ratio
ddod /dicos
varies in the range:
|
The regular faces of the series of solids are hexagonal faces of icosahedron if:
when the ratio ddod /dicos
varies in the range:
|
|
The regular faces of the series of solids are decagonal faces of dodecahedron if:
when the ratio
ddod /dicos varies in the range:
|
|
The regular faces of the series of solids are square faces of rhomb-triacontahedron if:
when the ratio
ddod /dicos varies in the range: |
Table C
The animated sequences, relative to each series of solids including the different kinds of regular faces,
are shown in the following images going from Fig. 15 to Fig. 18.
|
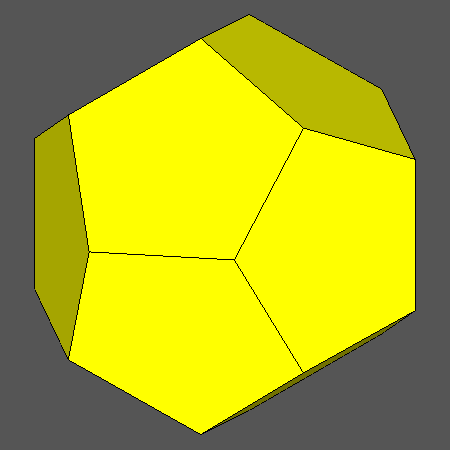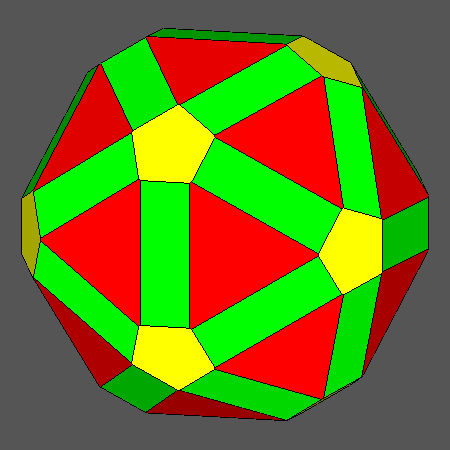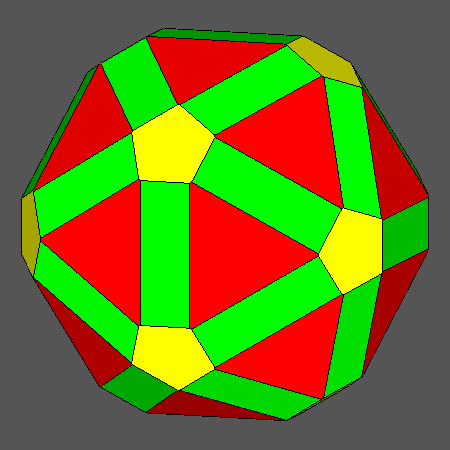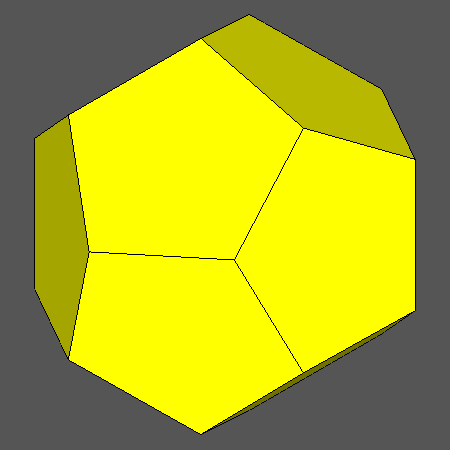
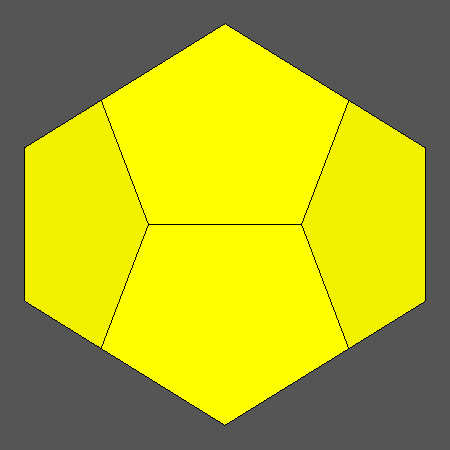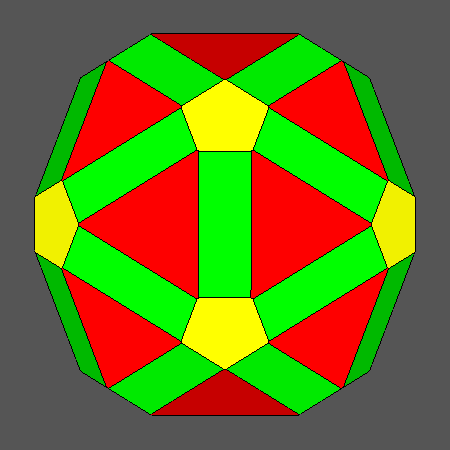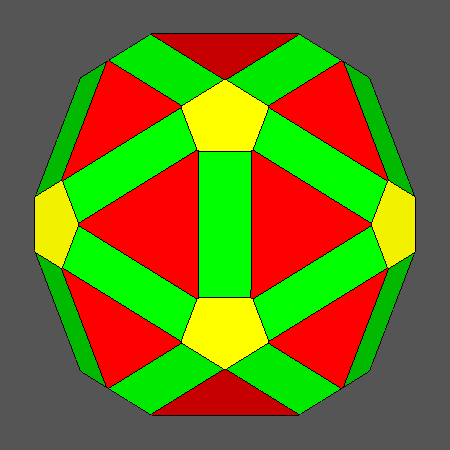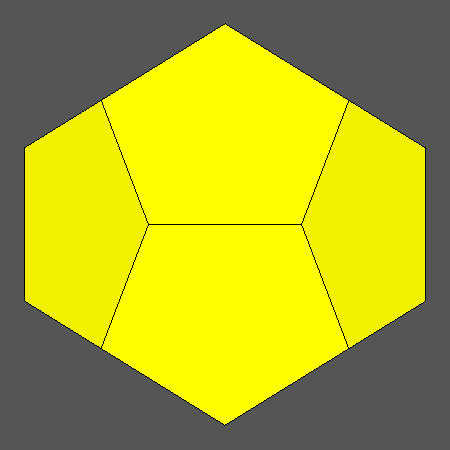
Set of vertex-transitive solids including pentagonal faces of dodecahedron and equilateral triangular faces of icosahedron
obtained when the ratio ddod/dicos varies in the range:
and the distance dRT is related to ddod and dicos by the relation:
|
 |
 |
|
Orthographic view of the sequence of vertex transitive solids, characterized by pentagonal faces of dodecahedron
and equilateral triangular face of icosahedron, going from the dodecahedron to the icosahedron
and including also the Archimedean rhomb-icosidodecahedron RID. |
View of the same sequence along the [100] 2-fold axis, normal to an usually rectangular face of each intermediate solid of the series.
It is only in case of the Archimedean rhomb-icosidodecahedron that all the rectangular faces become square. |
Fig. 15
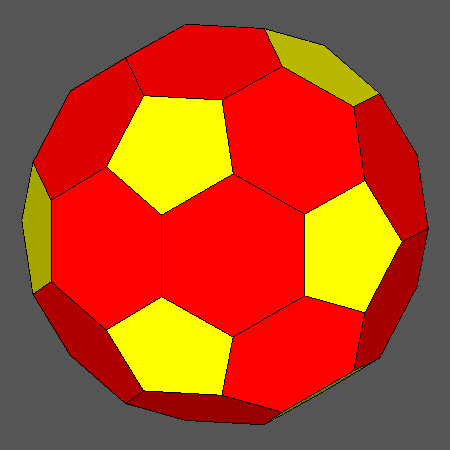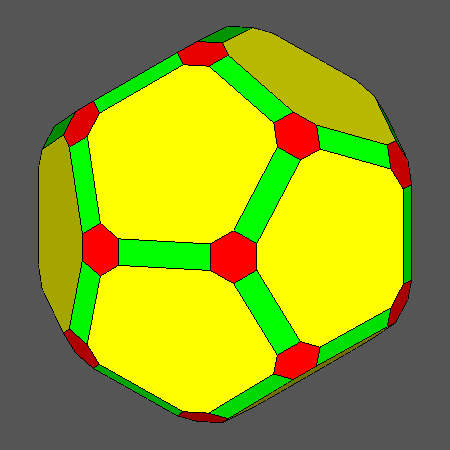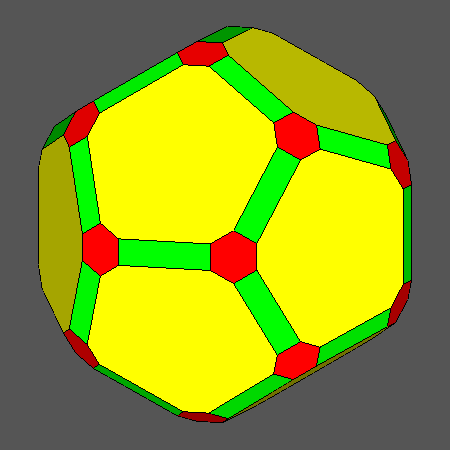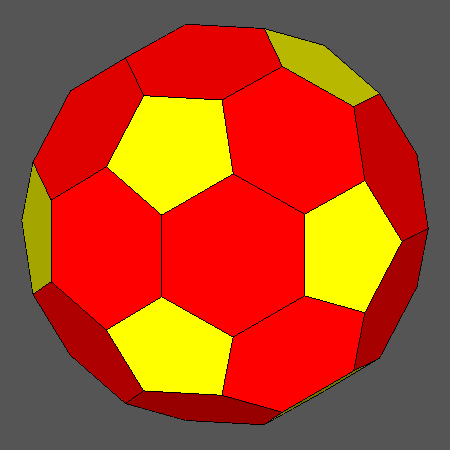
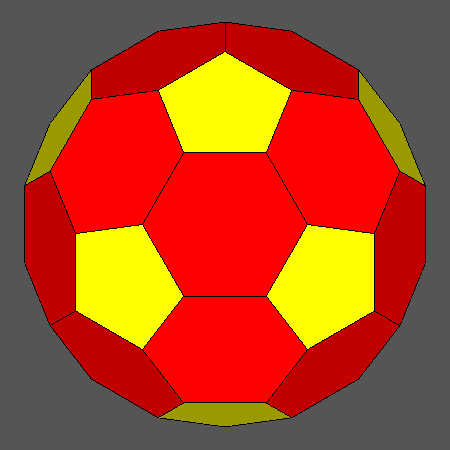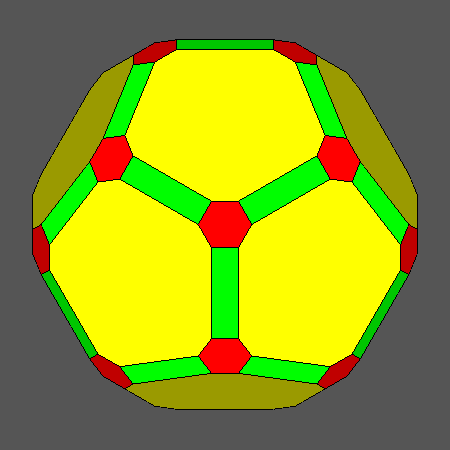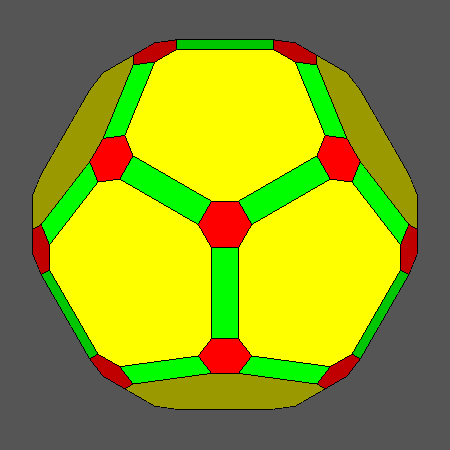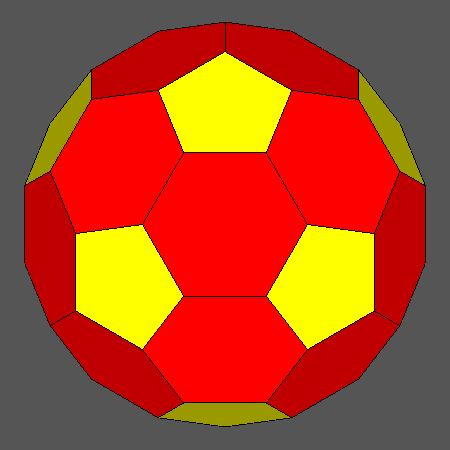
Set of vertex-transitive solids including regular hexagonal faces of icosahedron obtained
when the ratio ddod/dicos varies in the range:
and the distance dRT is related to ddod and dicos by the relation:
|
 |
 |
|
Orthographic view of the sequence of solids, characterized by regular hexagonal faces of icosahedron,
going from the Archimedean truncated icosahedron AtI to the dodecahedron and including also
the Archimedean truncated icosidodecahedron tID.
|
View of the same sequence along the [111] 3-fold axis, normal to a face of icosahedron having a regular hexagonal shape. |
Fig. 16
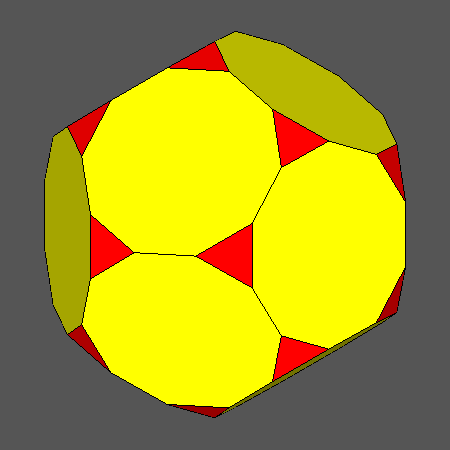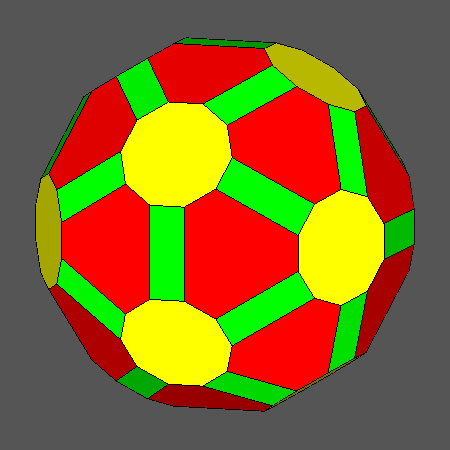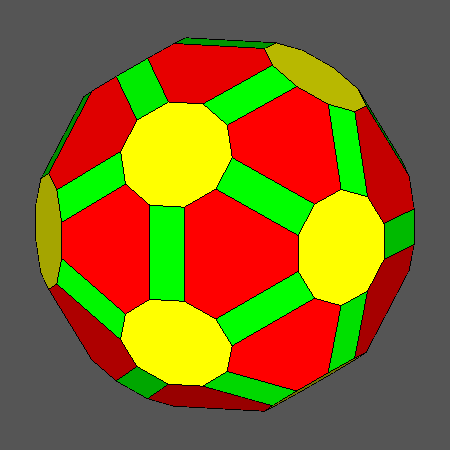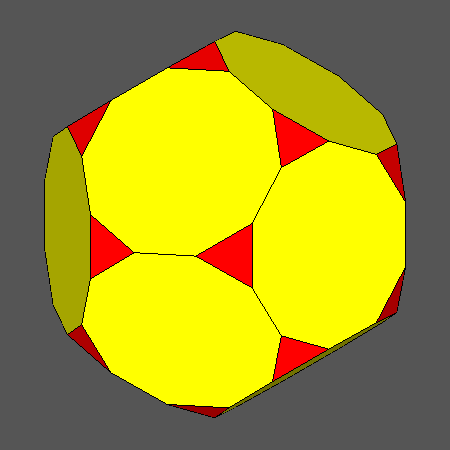
Set of vertex-transitive solids including regular decagonal faces of dodecahedron
obtained when the ratio ddod/dicos varies in the range:and the distance dRT is related to ddod
and dicos by the relation:
|
 |
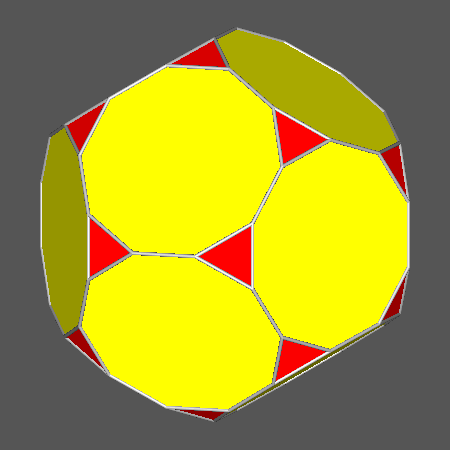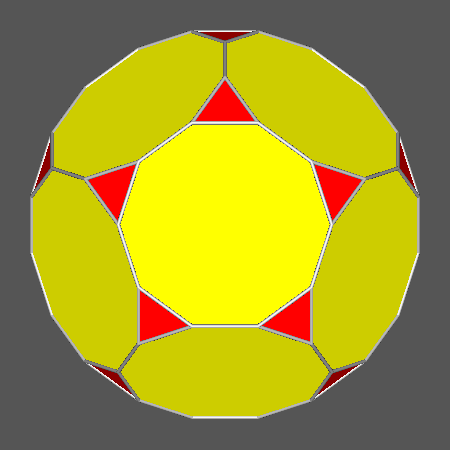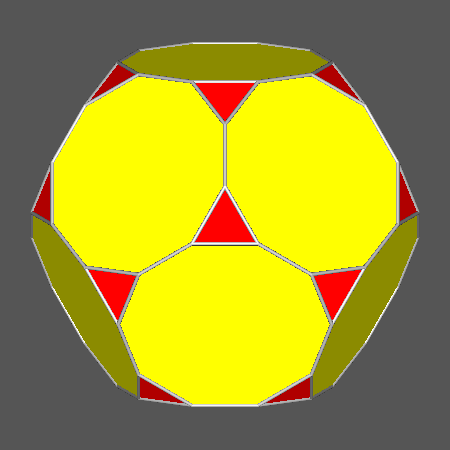
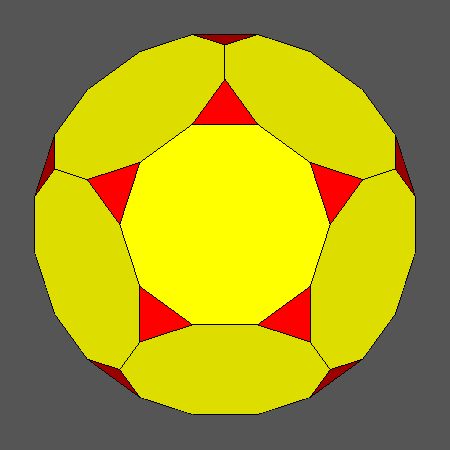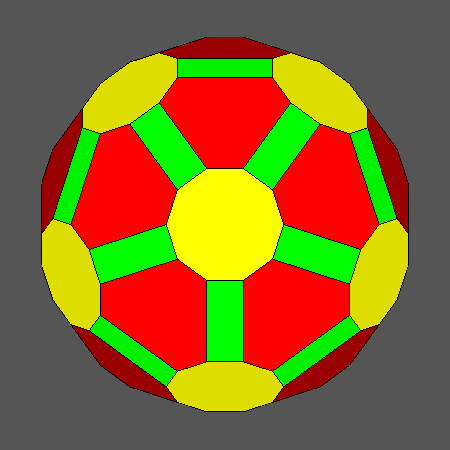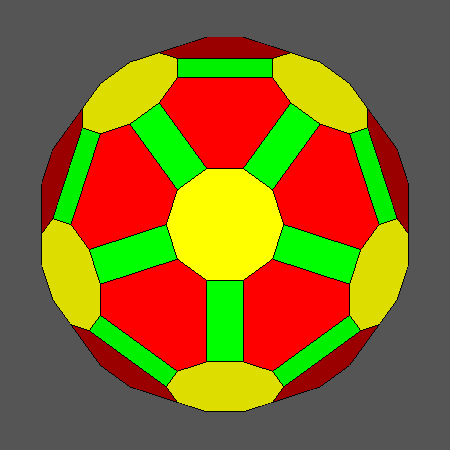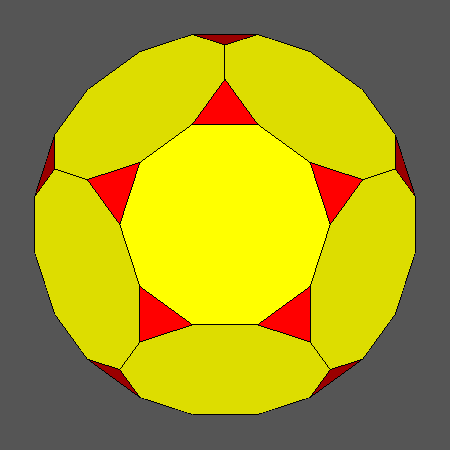 |
|
Orthographic view of the sequence of solids, characterized by regular decagonal faces of dodecahedron, going from the Archimedean truncated
dodecahedron AtD to the icosahedron and including also the Archimedean truncated icosidodecahedron tID.
|
View of the same sequence along the [τ01] 5-fold axis, normal to a face of dodecahedron having a regular decagonal shape. |
Fig. 17
Set of vertex-transitive solids including square faces of rhomb-triacontahedron obtained
when the ratio ddod/dicos varies in the range:
and the distance dRT is related to ddod and dicos by the relation:
|
 |
 |
|
Orthographic view of the sequence of solids characterized by square
faces of rhomb-triacontahedron RT, going from the icosidodecahedron ID to the rhomb-icosidodecahedron RID
and including also the truncated icosi-dodecahedron tID. |
View of the same sequence along the [100] 2-fold axis, normal to a square face of rhomb-triacontahedron. |
Fig. 18
LINKS
- Zefiro L.
Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra
VisMath, volume 13, No. 2, 2011
- Zefiro L.
Regular-shaped faces in solids with cubic symmetry derived from truncation processes by rhomb-dodecahedron or cube
VisMath, volume 13, No. 2, 2011
- Hart G.W.
Archimedean duals
Encyclopedia of Polyhedra
- Zefiro L., Ardigo' M.R.
Platonic and Catalan polyhedra as archetypes of forms belonging to the cubic and icosahedral systems
VisMath, volume 11, No. 2, 2009
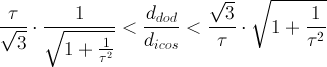
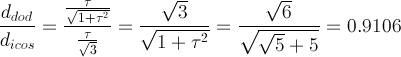


_&d(icos)_AtI.gif)
_&d(icos)_AtD.gif)

_su_d(icos)_ID.gif)
_su_d(icos)_AtI.gif)
_su_d(icos)_AtD_.gif)
_AtD_.gif)
_AtI_xtab.gif)
_su_d(icos)_RID_.gif)

_su_d(icos)_tID_.gif)
_su_d(RT)_tID.gif)
_su_d(icos)_RID_x_tab_.gif)
_su_d(icos)_tID_xtab_.gif)




























_.png)
_.png)
_450px.png)
_.png)
_bis_white_faces.png)











_300px.png)
_300px.png)
_300px.png)
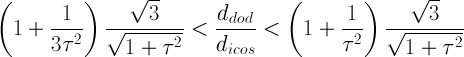



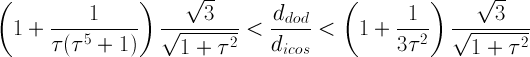



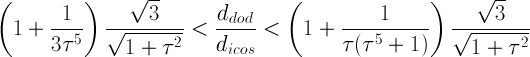



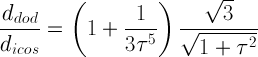






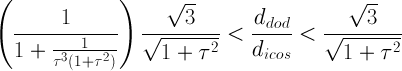



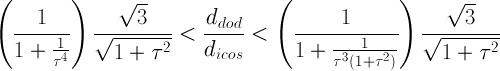



_1.gif)
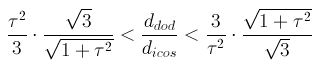
_2.gif)
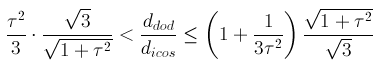
_3.gif)