Three mathematical animations
- Borromean and Brunnian Rings
- Boy's Surface
- Icosahedron and metamorphoses of a Paper dragon
Links to animations and additional information
link,
link2 and
Youtube
-
link1
-
link2
-
link3.
All three animations were created by Dušan Živaljević with (mathematical) assistance of his father (Rade Živaljević).
All three animations illustrate important mathematical concepts. They were created as part of the project MathAlive (Živa matematika), with R. Živaljević as the project leader. The project was supported by the Serbian Ministry of Science and Technology, the Centre for the Popularisation and Promotion of Science, and the Mathematical Institute SANU.
(1) Borromean and Brunnian Rings
(the link to the popular article (in Serbian)
The Borromean rings, named after the Italian Borromeo family, represent a fragile unity where if any of the rings is destroyed, the remaining two fall apart. (We get Brunnian rings if we entangle even a larger number of rings, keeping a similar „all for one, and one for all“ property.)
The Figure on the right exhibits the Borromean rings while on the left is the logo of the International Mathematical Union.
The animation of “Borromean rings“ offers a closely related interpretation of the “Borromeo phenomenon“. It illustrates how one can hang a painting on the wall, using more than one hook, with a paradoxical property that after removing any of the hooks, the painting is no longer supported (it falls down). The following pictures explain the connection between the two interpretations.
(2) Boy's surface
(the link to the article (in Serbian) about Boy’s surface)
The animation of the Boy’s surface illustrates a strange phenomenon that our 3-dimensional space is not ample (spacious) enough to allow the existence of closed, one-sided surfaces. For this to happen, we need a more spacious, 4-dimensional space. Indeed, all known closed surfaces that we meet in nature, such as balloons or bicycle tires, are two sided and for each of them we know what is inside and what is outside.
Moebius strip, exhibited in Figure 2, is one-sided, but it cannot be extended to a closed surface in our 3-dimensional space. However, if we allow the surface to self-intersect, then we can embed a one-sided surface in the 3-space, as demonstrated by the animation.
(Boy’s surface sculpture)
(3) Icosahedron and metamorphoses of a Paper dragon
The main character of this animation is a kite (paper dragon), made of 20 equilateral triangles, peacefully floating through the space. The dragon wakes up and begins to coil by bending its body along the edges of the adjacent triangles. The initial bending angle is 180 degrees and, as this angle gets smaller and smaller, the dragon attains different geometric forms, among them the tetrahedron (corresponding to the angle 70,530), octahedron (corresponding to the angle 109,470), icosahedron (the angle is 138,190), the ouroboros form when it bites its tail (the angle is 1500), and stellated dodecahedron.
Since the icosahedron has precisely 20 triangular faces, we see from the animation that the dragon wraps around the icosahedron without overlaps. We also observe that an icosahedral dice, known from ancient times, can be rolled so that it falls on each face exactly once.
Icosahedron, as a mathematical object, is very important for applications. It is known that outer shells (capsids) of a large number of viruses (including Covid 19), have the form of the icosahedron. Stable, self-assembling, non-infective structures of this type, as potential candidates for vaccines, are studied by mathematical virology.
https://www.pnas.org/content/101/44/15556
Gallery
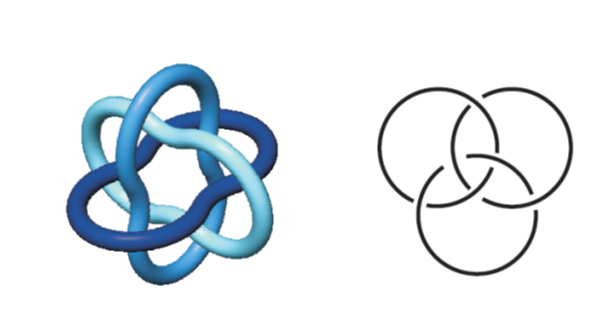
Borromean and Brunnian Rings
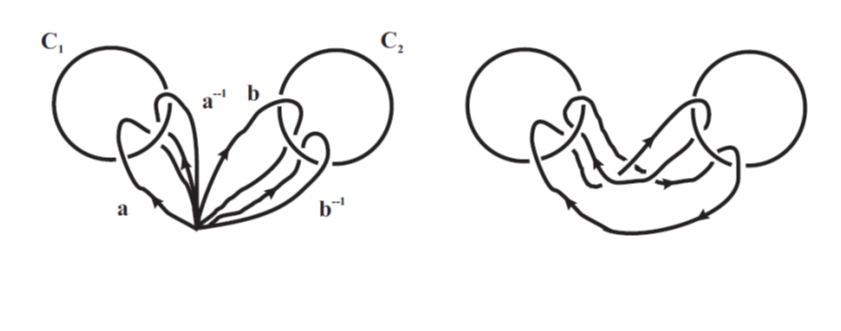
Borromean and Brunnian Rings

Boy’s surface sculpture
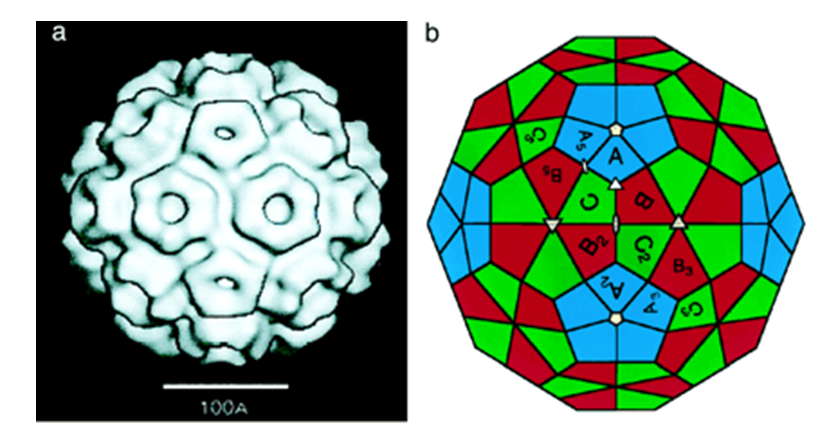
Icosahedron and metamorphoses of a Paper dragon


